量子计算的数学基础
Abstract vector space
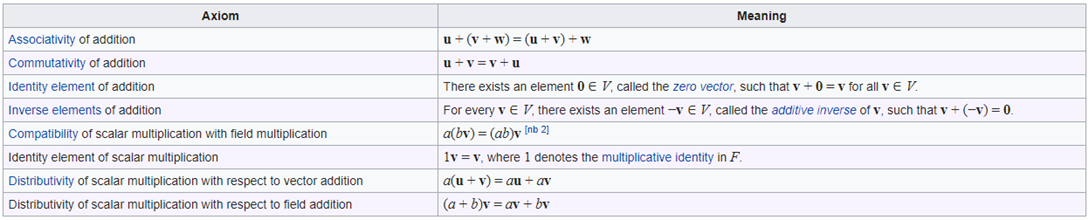
向量空间需要满足以下几个公理。向量空间中的元素即向量。
Inner product and Hilbert space
定义 \(\ket{\phi}\) 和 \(\ket{\psi}\) 的内积为:
- 若 \(\ket{\phi}\) 和 \(\ket{\psi}\) 是函数:
\[ \braket{\phi|\psi}=\int_{-\infty}^{+\infty}\bar{\phi}(x)\psi(x) dx \]
- 若 \(\ket{\phi}\) 和 \(\ket{\psi}\) 是列向量:
\[ \braket{\phi|\psi}=\phi^\dagger\psi=\bar{\phi}^T\psi \]
内积的物理解释:如果粒子的初始态为 \(\ket{\phi}\),那么在 \(\ket{\psi}\) 态发现该粒子的概率为 \(|\braket{\phi|\psi}|^2\)
希尔伯特空间即一个带内积的复向量空间
Qubits
Qubit 满足以下两个性质:
- Nomalized(归一的):
\[ \braket{0|0}=1, \braket{1|1}=1 \]
- Orthogonal(正交的):
\[ \braket{0|1}=0, \braket{1|0}=0 \]
因此,qubit 形成了 Hilbert 空间的一个基,即任何量子态都能用 \(\ket{0}\) 和 \(\ket{1}\) 的线性组合表示。
qubit 内积也可以表示为:
\[ \braket{i|j}=\delta_{ij} \]
\(\delta_{ij}\) 即为 Kronecker delta,满足
\[ \delta_{ij}= \begin{cases} 0, i\neq j \\ 1, i=j \end{cases} \]
Superposition of states
叠加态即为 qubit 的线性组合
\[ \braket{\psi}=\alpha\ket{0}+\beta\ket{1} \]
其中,\(|\alpha|^2+|\beta|^2=1\),且 \(|\alpha|^2\) 表示 \(\ket{0}\) 测量出的概率。
Tensor product
两个向量的张量积即为
\[ u\otimes v= \left[\begin{array}{c} u_1 \\ u_2 \end{array}\right]\otimes \left[\begin{array}{c} v_1 \\ v_2 \end{array}\right]= \left[\begin{array}{c} u_1\left[\begin{array}{c} v_1 \\ v_2 \end{array}\right] \\ u_2\left[\begin{array}{c} v_1 \\ v_2 \end{array}\right] \end{array}\right]= \left[\begin{array}{c} u_1v_1 \\ u_1v_2 \\ u_2v_1 \\ u_2v_2 \end{array}\right] \]
使用 Dirac 符号表示即为
\[ \ket{\psi}\otimes\ket{\phi}\equiv\ket{\psi}\ket{\phi}\equiv\ket{\psi,\phi}\equiv\ket{\psi\phi} \]
张量积具有如下性质
\[ (v+w)\otimes u = v\otimes u+w\otimes u \\ u\otimes(v+w) = u\otimes v+u\otimes w \\ c(v\otimes u) = (cv)\otimes u = v\otimes(cu) \]
张量积是不能交换的!!
Inner product on the tensor products
Suppose \(\ket{\psi_1}, \ket{\phi_1}\in H_1\) and \(\ket{\psi_2}, \ket{\phi_2}\in 𝐻_2\) where \(𝐻_1\) and \(𝐻_2\) are two Hilbert spaces. Then
\[ \braket{\phi_1,\phi_2|\psi_1,\psi_2}=\braket{\phi_1|\psi_1}_1\braket{\phi_2|\psi_2}_2 \]
Where \(\braket{\cdot|\cdot}_1\) and \(\braket{\cdot|\cdot}_2\) are inner product defined on \(𝐻_1\) and \(𝐻_2\), respectively.
Example:
\[ \braket{01|01}=\braket{0|0}\braket{1|1}=1\cdot1=1 \\ \braket{011|010}=\braket{0|0}\braket{1|1}\braket{1|0}=1\cdot1\cdot0=0 \]
Outer product
The outer product of two vectors \(\ket{\psi}\) and \(\ket{\phi}\) are defined as \(\ket{\psi_1}\bra{\phi}=\ket{\psi_1}\otimes\bra{\phi}\)
Outer product is used to produce operators (算符).
Example:
Let \(\ket{\psi}=\sqrt{1/2}\ket{0}+\sqrt{1/2}\ket{1}\). Then \(\hat{𝑃}_0\equiv\ket{0}\bra{0}\) is a projection operator (投影算符) and it projects the wave function onto \(\ket{0}\) state.
\[ \hat{𝑃}_0\ket{\psi}=\sqrt{1/2}\ket{0}\bra{0}\ket{0}+\sqrt{1/2}\ket{0}\bra{0}\ket{1}=\sqrt{1/2}\ket{0} \]
Eigenvalues and Eigenvectors
Let \(\hat{A}\) be an operator. If
\[ \hat{A}\ket{\psi}=\lambda\ket{\psi} \]
Then \(\lambda\) is an eigenvalue (特征值) of \(\hat{A}\) and \(\ket{\psi}\) is an eigenvector (特征向量) associated with \(\lambda\).
Example:
Find the eigenvalues and eigenvectors of projection operator \(\hat{𝑃}_0\equiv\ket{0}\bra{0}\)
Solution: Eigenvalues are 1 and 0, cooresponding eigenvectors are \(\ket{0}\) and \(\ket{1}\).
\[ \hat{𝑃}_0\ket{0}=1\cdot\ket{0} \\ \hat{𝑃}_0\ket{1}=0\cdot\ket{1} \]
Spectral theorem
Suppose the eigenvalues \(\lambda_1,\lambda_2,...,\lambda_n\) of \(\hat{A}\) are real, and their corresponding eigenvectors are \(\ket{\psi_1},\ket{\psi_2},...,\ket{\psi_n}\). Then the operator \(\hat{A}\) can be written as
\[ \hat{A}=\sum_{i=1}^n\lambda_i\ket{\psi_i}\bra{\psi_i} \]
Moreover, \(\{\ket{\psi_1},\ket{\psi_2},...,\ket{\psi_n}\}\) form a complete basis for the Hilbert space \(\hat{A}\) living in.
Sometimes, this is called spectral decomposition of operator \(\hat{A}\).
Completeness relation
From spectral theorem, we can easily get the so-called completeness relation:
\(\{\ket{\psi_1},\ket{\psi_2},...,\ket{\psi_n}\}\) is a complete basis
if and only if
\[ I=\sum_{i=1}^n\ket{\psi_i}\bra{\psi_i} \]
Where 𝐼 is an identity matrix.
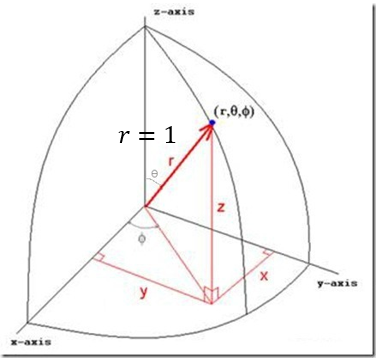
Bloch Sphere
The coefficients of a normalized quantum states must satisfy
\[ \ket{\psi}=\alpha\ket{0}+\beta\ket{1},\text{with }|\alpha|^2+|\beta|^2=1 \]
A normalized quantum state must be on a “sphere” (Bloch sphere). This sphere is called Bloch sphere.
Using polar angle \(\theta\), and azimuthal angle \(\phi\), we can write
\[ \ket{\psi}= \left[\begin{array}{c} \cos\frac{\theta}{2} \\ e^{i\theta}\sin\frac{\theta}{2} \end{array}\right] \]
Besides, in Cartesian coordinate system, we can write
\[ \begin{cases} x = \sin\theta\cos\phi \\ y = \sin\theta\sin\phi \\ z = \cos\theta \end{cases} \]

Global and relative phase
In computational basis, we can express a quantum state as
\[ \ket{\psi}=e^{i\gamma}(\cos\frac{\theta}{2}\ket{0}+e^{i\phi}\sin\frac{\theta}{2}\ket{1}) \]
Where \(e^{i\gamma}\) is called global phase, \(e^{i\phi}\) is called relative phase.
- Global phase DOES NOT affect anything (we can ignore it).
- Relative phase IS important, DO NOT forget it.
Example:

Unitary operators
An operator \(U\) is unitary if and only if \(U^\dagger U=UU^\dagger=I\).
Unitary operator PRESERVES the norm:
\[ ||U\ket{\psi}||^2=\bra{\psi}U^\dagger U\ket{\psi}=\bra{\psi}\ket{\psi}=||\ket{\psi}||^2 \]
In other words, unitary operators keep quantum states on the Bloch sphere.
Examples:
Pauli matrices:
\[ \sigma_x=X= \left[\begin{array}{c c} 0 & 1 \\ 1 & 0 \end{array}\right], \sigma_y=Y= \left[\begin{array}{c c} 0 & -i \\ i & 0 \end{array}\right], \sigma_z=Z= \left[\begin{array}{c c} 1 & 0 \\ 0 & -1 \end{array}\right], \]
Rotation about arbitrary axis
Pauli-Euler relation:
\[ \exp(i\alpha\hat{n}\cdot\vec{\sigma})=\cos(\alpha)I+i\sin(\alpha)\hat{n}\cdot\vec{\sigma} \]
where \(\hat{n}\) is a unit vector in \(\mathbb{R}^3\).
\(\vec{\sigma}=X\hat{x}+Y\hat{y}+Z\hat{z}\) is a vector of Pauli matrices.
For example:
\[ \hat{x}\cdot\vec{\sigma}=X= \left[\begin{array}{c c} 0 & 1 \\ 1 & 0 \end{array}\right] \]
To rotate a state \(\ket{\psi}\) along unit vector \(\hat{n}\) with angle \(\alpha\), multiply the rotation matrix \(R_{\hat{n}}(\alpha)\),
\[ R_{\hat{n}}(\alpha)\ket{\psi}=\exp(-i\frac{\alpha}{2}\hat{n}\cdot\vec{\sigma})\ket{\psi} \]

Pure state and mixed state
A pure state is a quantum state can be represented as a single vector.
That means, all vectors on the surface Bloch sphere are pure states! Since they can be written as
\[ \ket{\psi}= \left[\begin{array}{c} \cos\frac{\theta}{2} \\ e^{i\theta}\sin\frac{\theta}{2} \end{array}\right] \]
A mixed state is a vector inside Bloch sphere.
Density matrix and Bloch vector
For a given pure state \(\ket{\psi}\), define the density operator as
\[ \rho=\ket{\psi}\bra{\psi} \]
Let \(\ket{\psi}=[\cos\frac{\theta}{2},e^{i\theta}\sin\frac{\theta}{2}]^T\), then we have
\[ \rho=\frac{1}{2} \left[\begin{array}{c c} 1+\cos\theta & e^{-i\phi}\sin\theta \\ e^{i\phi}\sin\theta & 1-\cos\theta \end{array}\right] =\frac{1}{2}(I+xX+yY+zZ)=\frac{1}{2}(I+\vec{r}_\rho\cdot\vec{\sigma}) \]
where \(\vec{\sigma}=(X,Y,Z)\) is the vector of Pauli matrices and
\[ \vec{r}_\rho=(x,y,z)=(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta) \]
is called the unit Bloch vector. It is the Cartesian representation of \(\ket{\psi}\).
Purity
Define purity of a quantum state \(\ket{\psi}\) as
\[ \gamma=Tr(\rho^2) \]
where \(\rho=\ket{\psi}\bra{\psi}\) is the density operator of \(\ket{\psi}\). * Purity measures how much a state is mixed. * \(1/d\leq\gamma\leq1\) where \(d\) is the dimension of the Hilbert space. * \(\gamma=1\) if it’s a pure state, \(\gamma=1/d\) if it’s a completely mixed state.
Suppose \(\vec{r}_1\) and \(\vec{r}_2\) are the Bloch vectors of two pure states \(\ket{\psi_1}\) and \(\ket{\psi_2}\), then
\[ |\braket{\psi_1|\psi_2}|^2=Tr(\rho_1\rho_2)=\frac{1}{2}(1+\vec{r}_1\cdot\vec{r}_2) \]
This formula relates the inner product in \(H\) and the inner product in \(\mathbb{R}^3\).
Example:
- Bloch sphere geometry
Suppose \(\braket{\psi_1|\psi_2}=0\) (orthogonal in \(H\)), how do they look like on Bloch sphere?
Using the formula,
\[ |\braket{\psi_1|\psi_2}|^2=\frac{1}{2}(1+\vec{r}_1\cdot\vec{r}_2) \]
Since \(\braket{\psi_1|\psi_2}=0\), so we have \(\vec{r}_1\cdot\vec{r}_2=-1\). \(\ket{\psi_1}\) and \(\ket{\psi_2}\) have opposite directions!
- Purity
Let \(\ket{\psi}=\frac{\ket{0}-\ket{1}}{\sqrt{2}}\), calculate its purity.
\[ \rho_{\psi}=\frac{1}{2}(\ket{0}\bra{0}-\ket{0}\bra{1}-\ket{1}\bra{0}+\ket{1}\bra{1})=\frac{1}{2}\left[\begin{array}{c c} 1 & -1 \\ -1 & 1 \end{array}\right] \\ \implies \rho_{\psi}^2=\frac{1}{4}\left[\begin{array}{c c} 2 & -2 \\ -2 & 2 \end{array}\right] \implies Tr(\rho_{\psi}^2)=1 \]
This is obvious, since \(\ket{\psi}\) can be drawn on Bloch sphere, so it is a pure state.