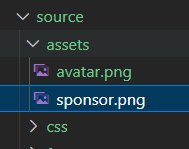
Quantum Circuits
量子电路即对 qubit 操作的图形表示,时间顺序为从左至右。有两种 qubit 操作:量子逻辑门(quantum logic gate)、测量(measurement)。
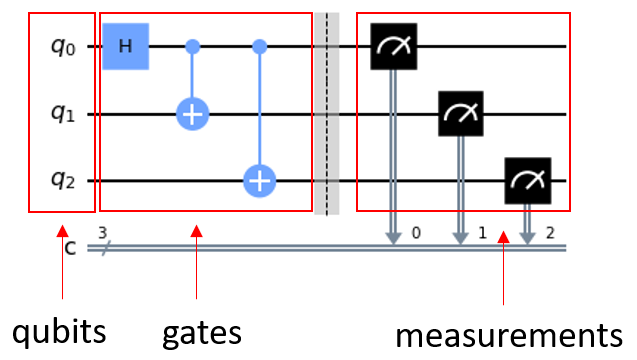
Quantum Logic Gates
所有的量子逻辑门都是酉算子(unitary operator)
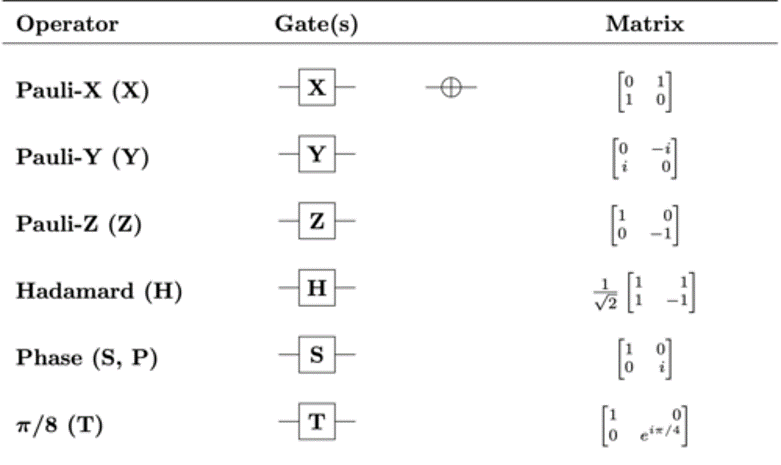
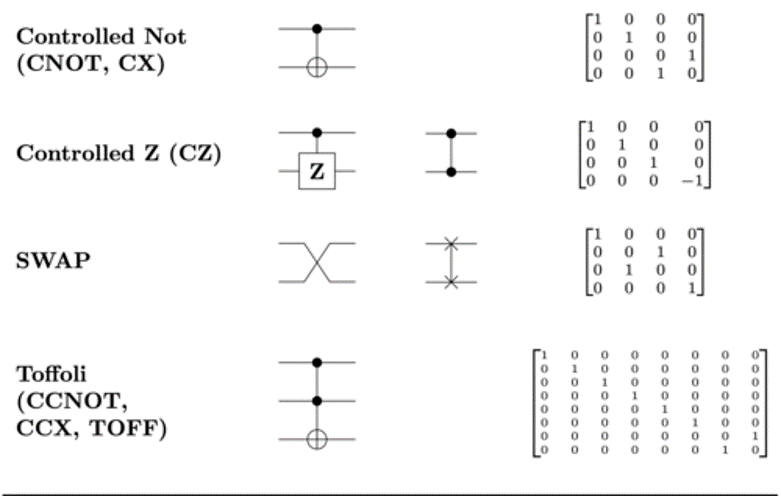
Example:
将 Pauli X matrix 作用于基底,可以得到相反的基底,所以 Pauli X matrix 也被称作 NOT 门
$$ \[\begin{align*} X\ket{0}=\left[\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}\right]\left[\begin{matrix} 1 \\ 0 \end{matrix}\right]=\left[\begin{matrix} 0 \\ 1 \end{matrix}\right]=\ket{1} \\ X\ket{1}=\left[\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}\right]\left[\begin{matrix} 0 \\ 1 \end{matrix}\right]=\left[\begin{matrix} 1 \\ 0 \end{matrix}\right]=\ket{0} \end{align*}\] $$
将 Hadamard gate 作用于基底,可以获得基底的叠加态
\[ \begin{align*} H\ket{0}=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 & 1 \\ 1 & -1 \end{matrix}\right]\left[\begin{matrix} 1 \\ 0 \end{matrix}\right]=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 \\ 1 \end{matrix}\right]=\frac{\ket{0}+\ket{1}}{\sqrt{2}} \\ H\ket{1}=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 & 1 \\ 1 & -1 \end{matrix}\right]\left[\begin{matrix} 0 \\ 1 \end{matrix}\right]=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 \\ -1 \end{matrix}\right]=\frac{\ket{0}-\ket{1}}{\sqrt{2}} \end{align*} \]
另外还有常用的 Controlled NOT gate(CNOT),这个门会根据第一个 qubit 的取值而决定是否往第二个 qubit 上作用 NOT 门,即第一个 qubit 为 0 时不作用,为 1 时作用。
\[ \begin{align*} &CX\ket{00}=\left[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{matrix}\right]\left[\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}\right]=\left[\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}\right]=\ket{00} \\ &CX\ket{01}=\ket{01} \quad CX\ket{10}=\ket{11} \quad CX\ket{11}=\ket{10} \quad \end{align*} \]
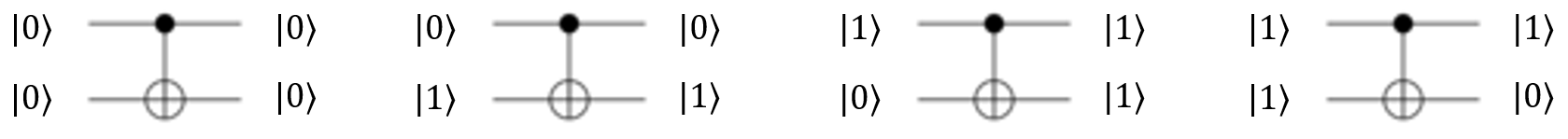
No-cloning Theorem
没有在 \(H\otimes H\) 上的酉算子 \(U\),能对 \(H\) 中的归一化状态 \(\ket{\psi}_A\) 和状态 \(\ket{e}_B\) 有如下的操作
\[ U(\ket{\psi}_A\ket{e}_B)=e^{i\alpha(\psi,e)}\ket{\psi}_A\ket{\psi}_B \]
Proof:
假设存在这样的 \(U\),那么有
\[ \begin{align*} U\ket{\psi}_A\ket{e}_B=\ket{\psi}_A\ket{\psi}_B \\ U\ket{\phi}_A\ket{e}_B=\ket{\phi}_A\ket{\phi}_B \end{align*} \]
将两式相点乘,可以得到
\[ \begin{align*} \text{left}=\bra{e}_B\bra{\psi}_AU^{\dagger} U\ket{\psi}_A\ket{e}_B=(\braket{\psi|\psi})_A(\braket{e|e})_B=\braket{\psi|\psi} \\ \text{right}=\bra{\psi}_B\bra{\psi}_A\ket{\phi}_A\ket{\phi}_B=(\braket{\psi|\phi})_A(\braket{\psi|\phi})_B=|\braket{\psi|\phi}|^2 \end{align*} \]
因此有
\[ \braket{\psi|\psi}=|\braket{\psi|\phi}|^2 \implies \braket{\psi|\psi}=0\text{ or }1 \]
所以除了互相正交的基底,我们不可能仅通过当前的状态情况复制该状态。
注意:这不意味着我们不可以复制量子状态,而是说不可能有人能窃听到量子通信中的信息。
Measurement
薛定谔的猫(Schrödinger's cat),只有当测量的时候才能知道真实的情况。
对 qubit 的测量会导致其以一定概率坍缩到确定的状态(\(\ket{0}\) 或 \(\ket{1}\)),但要获得最终结果,必须要测量 qubit
Example:
测量如下的 qubit,将会得到什么预期结果呢?
\[ H\ket{1}=\frac{\ket{0}-\ket{1}}{\sqrt{2}} \]
预期情况下,会有 50% 的概率测量得到 \(\ket{0}\),会有 50% 的概率测量得到 \(\ket{1}\)
一般来说,对 qubit \(\ket{\psi}=\alpha\ket{0}+\beta\ket{1}\),会有 \(|\alpha|^2\) 的概率测量得到 \(\ket{0}\),会有 \(|\beta|^2\) 的概率测量得到 \(\ket{1}\)。而对归一化的 qubit 来说,\(|\alpha|^2+|\beta|^2=1\)
Reversibility in Quantum Computing
函数是可逆的(reversible)当且仅当它是双射的(bijective)。
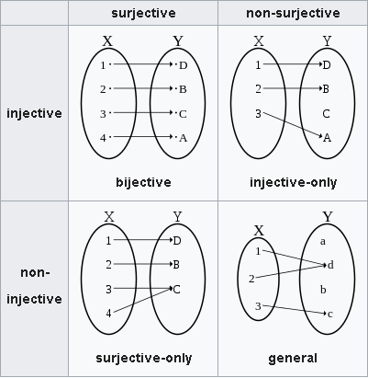
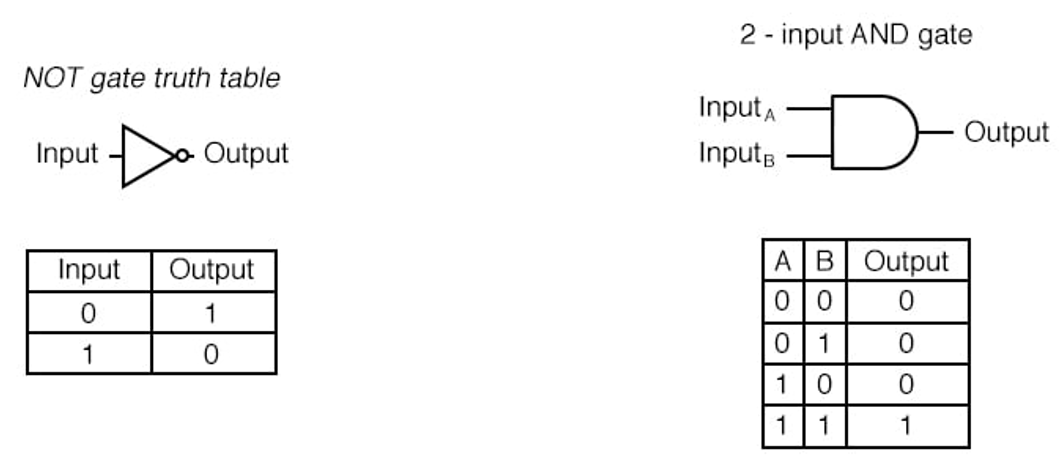
经典计算机中的逻辑门不一定是可逆的,如 NOT 门、AND 门,将它们作用于 bit 之后,会丢失一些信息。
但我们可以通过添加一些辅助 bit 将逻辑门转化成可逆的。
假设 \(f:i\to f(i)\) 有 \(n\) 个 输入和 \(m\) 个输出,我们需要增加额外 \(n\) 个 输出和 \(m\) 个输入,并将函数改为 \(f_{rev}:i,j\to i,f(i)\oplus j\),其中 \(\oplus\) 为 XOR
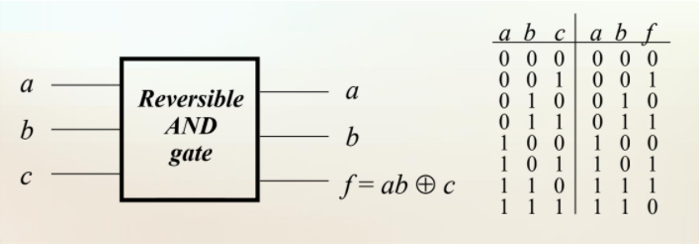
量子电路中的逻辑门必须是酉的(unitary),而逻辑门 \(U\) 的逆是唯一的,即 \(U^{\dagger}\)
Example:
Hadamard 门的逆
\[ \begin{align*} H\ket{0}=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 & 1 \\ 1 & -1 \end{matrix}\right]\left[\begin{matrix} 1 \\ 0 \end{matrix}\right]=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 \\ 1 \end{matrix}\right]=\frac{\ket{0}+\ket{1}}{\sqrt{2}} \\ H^{\dagger}\frac{\ket{0}+\ket{1}}{\sqrt{2}}=\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 & 1 \\ 1 & -1 \end{matrix}\right]\frac{1}{\sqrt{2}}\left[\begin{matrix} 1 \\ 1 \end{matrix}\right]=\left[\begin{matrix} 1 \\ 0 \end{matrix}\right]=\ket{0} \end{align*} \]
要将经典电路中的逻辑门改成量子电路中的逻辑门,可根据先前所说的增加一些辅助 qubit 即可。
量子 AND 门、量子 NAND 门
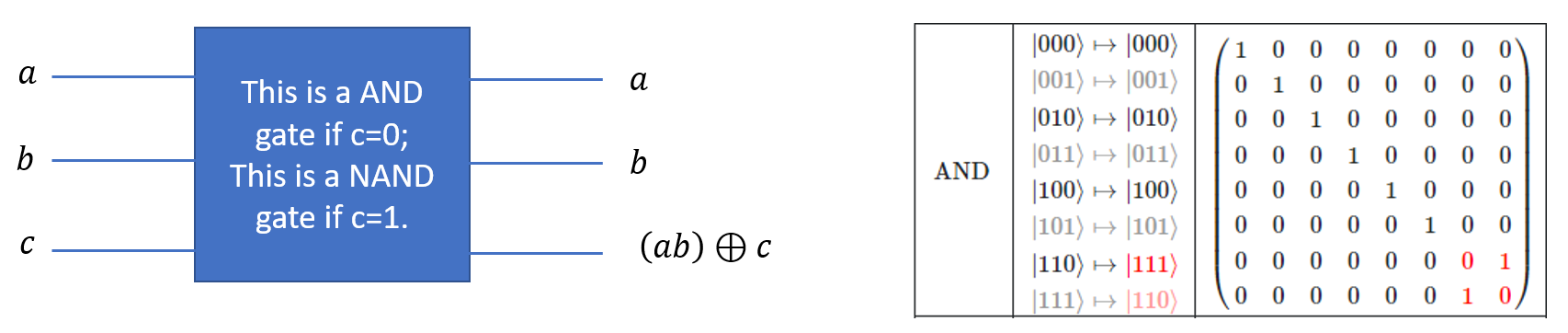
量子 OR 门、量子 NOR 门
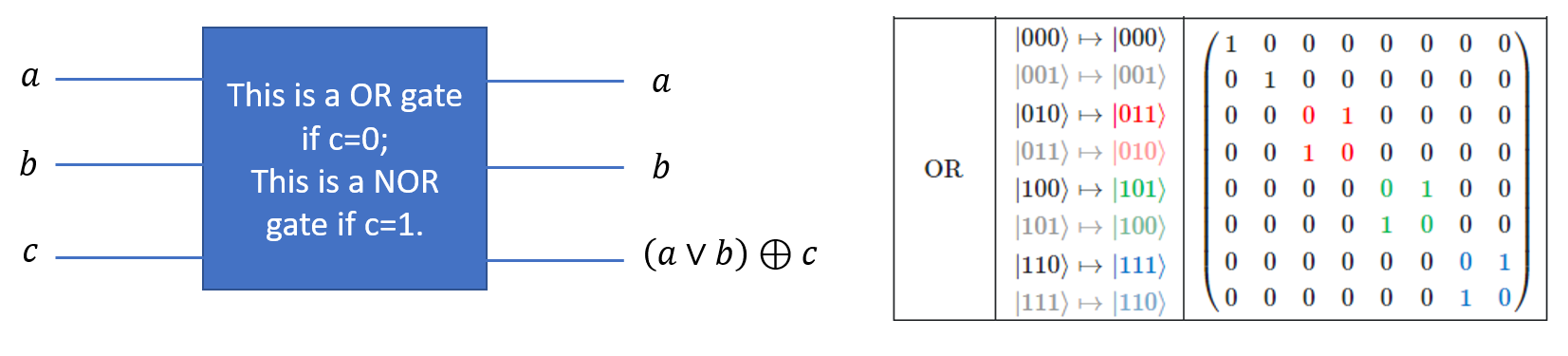
Universal Gate Sets
我们可以通过有限的门数,将任意酉算子近似到任意给定的精度(类似于泰勒展开式)。
完成这项工作的门的集合被称为通用门集合(universal gate set),如
- {Hadamard,Phase,\(\pi/8\),CNOT}
- {Hadamard,Phase,Toffoli,CNOT}
Decomposition of Unitary Matrix
一个 \(d\) 维的酉矩阵 \(U\) 可被分解为二级酉矩阵的乘积
\[ U=V_1V_2...V_k \]
其中 \(k\le(d-1)+(d-2)+...+1=d(d-1)/2\)
这意味着我们可以用二级酉矩阵来表示任意酉矩阵。
具体推导可以参考文章 Decomposition of unitary matrices and quantum gates