归约(reduction)是指问题 A 的任何实例能用问题 B 的方法来解决(判断),并且 A 的解为 true,当且仅当 B 的解也是 true。此时可标为 \(A\leq_p B\)。也就是说,归约可以将难以直接证明(或直接证明较为复杂)的问题转化为证明另一个较为简单问题。
密码学中的归约证明
在现代密码学中要证明方案或协议的安全性,常常使用 game 的形式来构造证明过程。归约证明(proof by reduction)就是其中的核心。
一般来说,一个密码学方案或协议 \(\Pi\) 是建立在已被证明安全的方案或协议,或者是某些困难问题之上(记为 \(X\))。困难问题就相当于地基,密码学方案或协议就相当于高楼。只要地基是稳固的,高楼一般就安全了。因此我们希望下面的命题是为真的:
Prop.1(命题):若 \(X\) 是安全的,那么方案 \(\Pi\) 就是安全的。若 \(X\) 被有效攻破,那么方案 \(\Pi\) 就不再安全。
实际上,这就是离散数学中假言命题的逻辑等价式:
\[ p\rightarrow q \equiv \neg q\rightarrow\neg p \]
同时这个等价式也是反证法的基础。因此,若要在归约证明中证明某一个新提出的方案 X 的安全性:
Thm.(定理):Y 是安全的 \(\rightarrow\) X 是安全的
也就是要证明:
Prop.2(命题):X 不是安全的 \(\rightarrow\) Y 不是安全的
进一步说:如果存在一个 PPT 的 attacker A 可以攻破 X,那么我们能构造一个 PPT 的 attacker B 来攻破 Y。其中,X 是新提出的方案,Y 是某一个困难问题,PPT 是多项式概率时间。“构造”一词可以理解为模拟。
如果能使条件命题 2 成立,那么就完成了归约证明。
证明过程
在密码协议的安全性证明中,一般使用 game 的方式来定义什么是安全的/不安全的。一个 game 中有两个 party,一个是 attacker,另一个是 challenger。attacker 试图破坏协议的安全,challenger 则是帮助构造协议的安全。
假设已知问题 \(X\) 难以解决,想要证明某构造方案 \(\Pi\) 安全,就要将成功攻破该方案 \(\Pi\) 的有效 attacker \(\mathcal{A}\) 转化为成功解决问题 \(X\) 的有效 attacker \(\mathcal{A}'\),这与 \(X\) 困难的假设相矛盾,所以方案 \(\Pi\) 无法被攻破,因此该方案是安全的。
其中 \(X\) 和 \(\Pi\) 分别有两个 party,即 \(X\) 的 challenger 和 attacker 与 \(\Pi\) 的 challenger 和 attacker。我们还需要分别以两个 game 来定义 \(X\) 和 \(\Pi\) 的安全性,且这两个 game 是互相独立的。在归约证明中,我们让 \(X\) 的 attacker 来模拟 \(\Pi\) 的 challenger,且要求:
- \(X\) 的 attacker 所模拟的 \(\Pi\) 的 challenger 够“逼真”,使得 \(\Pi\) 的 attacker 无法区分它的 challenger 是真实的还是模拟的,除了 negligible 的概率;
- 所模拟的 \(\Pi\) 的 challenger 是 PPT 的。
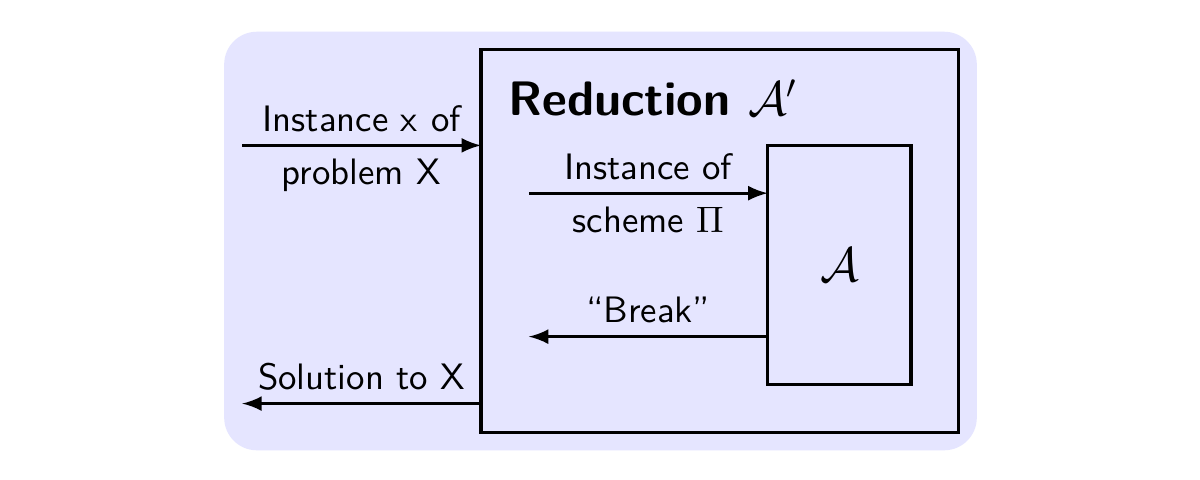
如上图所示,证明的过程如下:
- 指定 PPT attacker \(\mathcal{A}\) 攻击方案 \(\Pi\),且成功的概率为 \(\varepsilon(n)\);
- 假设:问题 \(X\) 难以解决,即无法在 PPT 内以 not negligible 的概率解决;
- 归约:构造 efficient attacker \(\mathcal{A}'\),它将 \(\mathcal{A}\) 当作 subroutine 运行,从问题 \(X\) 的实例 \(x\) 模拟出一个 \(\Pi\) 的实例,输入给 \(\mathcal{A}\)。如果 \(\mathcal{A}\) 被成功攻破,则 \(\mathcal{A}'\) 成功解决实例 \(x\) 的概率至少为多项式的倒数 \(1/p(n)\);
- 矛盾:那么 \(\mathcal{A}'\) 解决问题 \(X\) 的概率为 \(\varepsilon(n)/p(n)\)。若 \(\varepsilon(n)\) not negligible,则 \(\varepsilon(n)/p(n)\) 也 not negligible,这与 \(X\) 困难的假设相矛盾。
- 结论:attacker \(\mathcal{A}\) 无法以 not negligible 的概率攻破方案 ,也即 \(\Pi\) 是 computationally secure 的。
通俗的说,在 attacker \(\mathcal{A}'\) 接收到外部的 challenger 的输入数据后,对其进行适当变换,然后模拟为 challenger,将变换后的数据输入给 attacker \(\mathcal{A}\)。然后 \(\mathcal{A}'\) 根据 \(\mathcal{A}\) 的输出,适当变换后输出给外部,完成这次的 challenge。可以看到,\(\mathcal{A}'\) 对 \(X\) 的 game(\(X\) 的安全性)转移到 \(\mathcal{A}\) 对 \(\Pi\) 的 game(\(\Pi\) 的安全性)上了。这样的转移即构成了命题中的 implies(\(\rightarrow\))。
证明例子
PRG
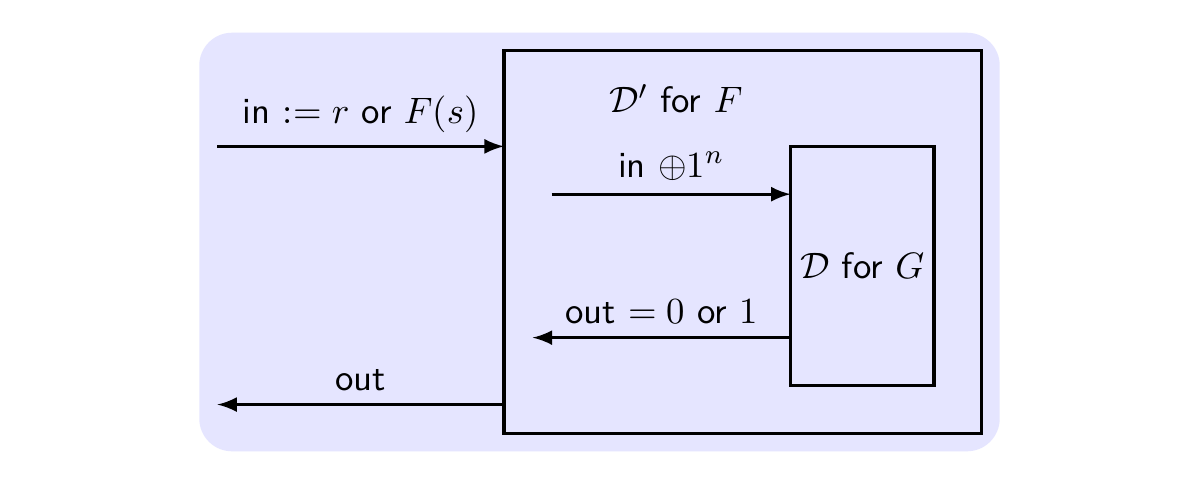
伪随机数发生器(pseudorandom generator, PRG)输入长度为 \(n\) 的种子 \(s\) ,算法 \(G\) 输出长度为 \(l(n)\) 的字符串。若无法区分它和均匀随机选择的字符串,则称其满足伪随机性。用数学语言描述就是,对于 PPT 的 distinguisher \(\mathcal{D}\) 来说,存在 negligible 函数 \(negl(n)\) 满足:
\[ |\Pr[D(r)=1]-\Pr[D(G(s))=1]|\le negl(n) \]
其中 \(r\) 是从 \(\{0,1\}^{l(n)}\) 中均与随机选择的,种子 \(s\) 是从 \(\{0,1\}^n\) 中均匀随机选择的。