NeRF(Neural Radiance Field)即神经辐射场。仅利用多个视角的 RGB 图像,训练神经网络构建一个隐式的三维表征,即可渲染得到模型没有见过的新视角下的图像。其主要贡献在于实现了神经场(Neural Field)与体渲染(Volume Rendering)的有效结合。
基础知识
表征方法
Soft Shape
这是 NeRF 成功及其重要的因素。
NeRF 使用了软不透明度场(soft opacity field)来生成形状,即从一片三维虚空中,按图像需要逐渐生成出具有特定结构三维物体。这样生成的形状不像 Mesh 等 Hard Geometry 一样具有确定性的空间边界,而是以一定概率连续地弥散在整个空间中的。


Soft Geometry 有两大好处:
- 不需要使用对象分割掩码(object segmentation masks);
- 没有边界不连续的(boundary discontinuity)问题,这意味着更易于做可微渲染。
同时也有一些缺点,如渲染成本高,编辑困难等等。

相关论文:
Radiance Field
给出每个表面点 \((x,y,z)\) 处不同的观察角度 \((\theta,\phi)\) 的颜色 \((r,b,g)\)。用这种方式可以很方便的描述物体表面的颜色,反射,和阴影等效果。但缺点是不易于修改和编辑。
相关论文:
以上这两种表征方法都可以视为空间中的函数,因此也方便后续使用神经网络来拟合。
方法概述
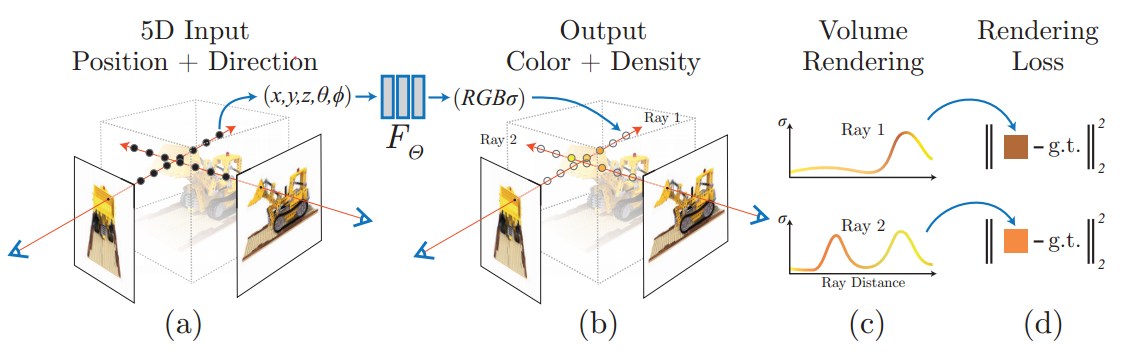
NeRF 工作的过程可以分成两部分:三维重建和渲染。
三维重建:从二维多视角图像构建三维场景(反渲染)
利用三维点的位置 \((x,y,z)\) 及方位视角 \((\theta, \phi)\) 作为输入,通过多层感知机(MLP)建模该点对应的颜色(Color,RGB)及体密度 (Volume Density,\(\sigma\)),该建模过程 \(F_\Theta\) 形成了三维场景的隐式表示。
渲染:计算某视角下的二维图像(体渲染)
使用可微分渲染器(Differentiable Renderer),利用重建部分得到的 Scene Representation 沿着 ray 结合得到最终的二维图像像素值.
在训练的时候,利用渲染部分得到的二维图像,通过优化与 Ground Truth 的 L2 Loss 训练网络。
Pipeline
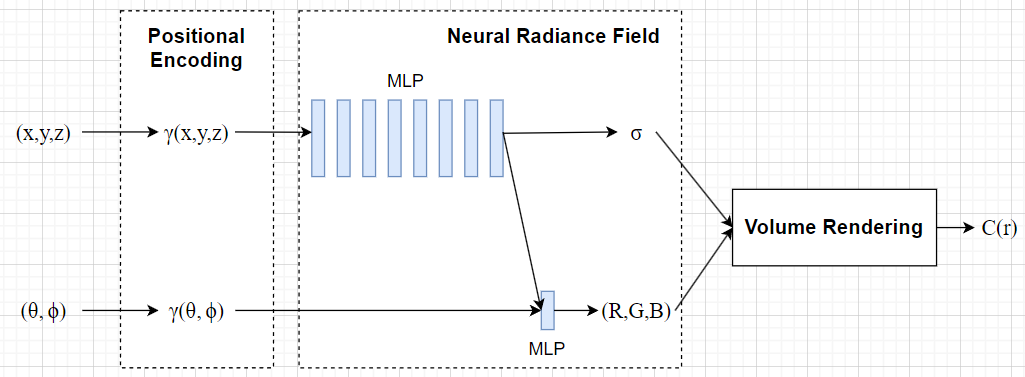
Neural Radiance Field Scene Representation
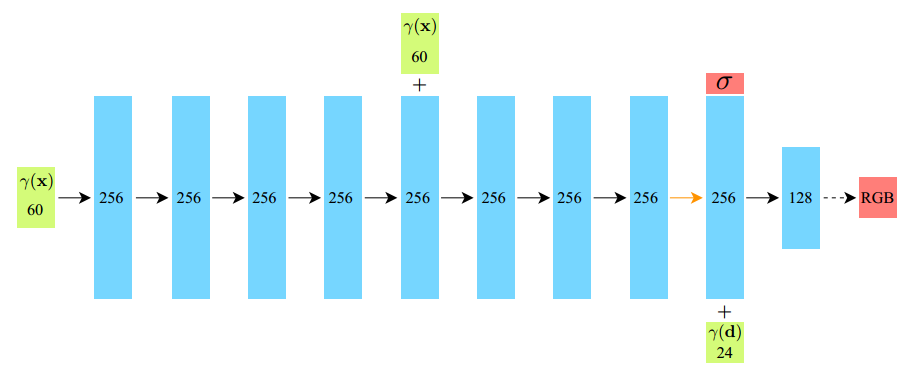
该部分的输入是三维位置 \((x,y,z)\) 和二维方位视角 \((\theta,\phi)\),输出是颜色 \(c=(r,g,b)\) 和体密度 \(\sigma\),即利用一个 MLP 网络近似地表示这种映射 \(F_\Theta: (x,d)\rightarrow(c,\sigma)\),这个映射 \(F_\Theta\) 就是一种三维场景的隐式表示。
该 MLP 网络先使用 8 层 256 通道的全连接层接收 \((x,y,z)\) 输入,并使用 ReLU 激活,输出 \(\sigma\) 和一个 256 维的向量。然后这个向量与 \((\theta,\phi)\) 连接,并输入 1 层 128 通道的全连接层,并使用 ReLU 激活,输出颜色 \(c=(r,g,b)\)。
Volume Rendering with Radiance Fields
我们可以将体密度 \(\sigma(\mathbf{x})\) 视为 ray 终止于位置 \(\mathbf{x}\) 的无限小粒子的微分概率。
在 ray \(\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}\) 上 \([t_n,t_f]\) 段的期望颜色 \(C(\mathbf{r})\) 为:
\[ C(\mathbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt,\text{ where }T(t)=\exp(-\int_{t_n}^t\sigma(\mathbf{r}(s))ds) \]
其中 \(T(t)\) 表示从 \(t_n\) 到 \(t\) 沿 ray 的累积透射率,即 ray 从 \(t_n\) 到 \(t\) 不碰到任何粒子的概率。
实际训练中,需要对积分进行离散化处理,NeRF 采用了 stratified sampling 方式(Monte Carlo 法的采样方法):将射线需要积分的区域分为 N 等份,然后在每一个小区域中进行均匀随机采样:
\[ t_i\sim\mathcal{U}[t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)] \]
离散化后,原渲染公式变为:
\[ \hat{C}(\mathbf{r})=\sum_{i=1}^NT_i(1-\exp(-\sigma_i\delta_i))\mathbf{c}_i,\text{ where }T_i=\exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j) \]
其中 \(\delta_i=t_{i+1}-t_i\) 为相邻样本间的距离。
关于体渲染的推导,可参考体渲染.
NeRF 在一条 ray 上采样多个不同的点,不同的点有各自的颜色,该颜色是通过神经网络预测出的。将 ray 上所有点的颜色结合起来,即可获得这个 ray 的颜色。
Positional encoding
尽管可以利用神经网络把表征的各种映射关系拟合成一个函数,比如映射成颜色的函数,映射成是否 occupy 的函数,映射成光照密度(density)的函数等等。
但问题是神经网络表示的是有偏的(bias),通过神经网络可能无法得到高质量的结果,如下图所示,它更偏向于得到光滑(smooth)的结果(也即学习低频信号),但我们期待的是得到锐利(sharp)的结果(也即学习高频信号)。因此 NeRF 提出了在将 \((x,y,z,\theta,\phi)\) 传递给网络之前,使用高频函数将输入映射到更高维度的空间,可以更好地拟合包含高频变化的数据。
NeRF 使用了一个具有傅里叶特征(Fourier features)的函数 \(\gamma\) 将 \(\mathbb{R}\) 数据映射到 \(\mathbb{R}^{2L}\),即 \(F_\Theta=F_\Theta'\circ\gamma\)。该高频编码函数为:
\[ \gamma(p)=(\sin(2^0\pi p),\cos(2^0\pi p),...,\sin(2^{L-1}\pi p),\cos(2^{L-1}\pi p)) \]
其中 \(p\) 就是 \((x,y,z,\theta,\phi)\) 输入,并且输入均归一化于 \([-1,1]\)。
根据这篇论文:
NeRF 对 \((x,y,z)\) 取 \(L=10\),对 \((\theta,\phi)\) 取 \(L=4\).
下图可以看出来,结果相较之前有十分明显的提升。

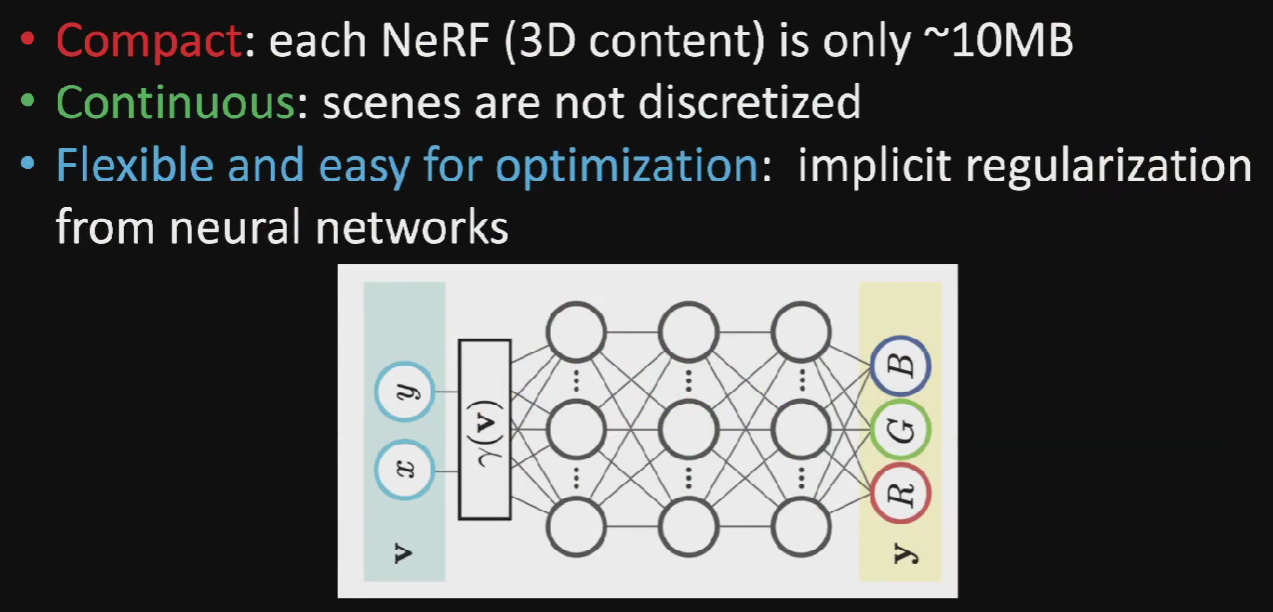
使用神经网络表示信号的方式,称为神经场(Neural Field)。这种方式有三个好处: 1. 每个三维模型大约只需要10MB就可以表示,利于传输; 2. 场景不需要离散化(discretized); 3. 更加灵活且易于优化:例如在正则化方面更方便,泛化能力更强。
Hierarchical volume sampling
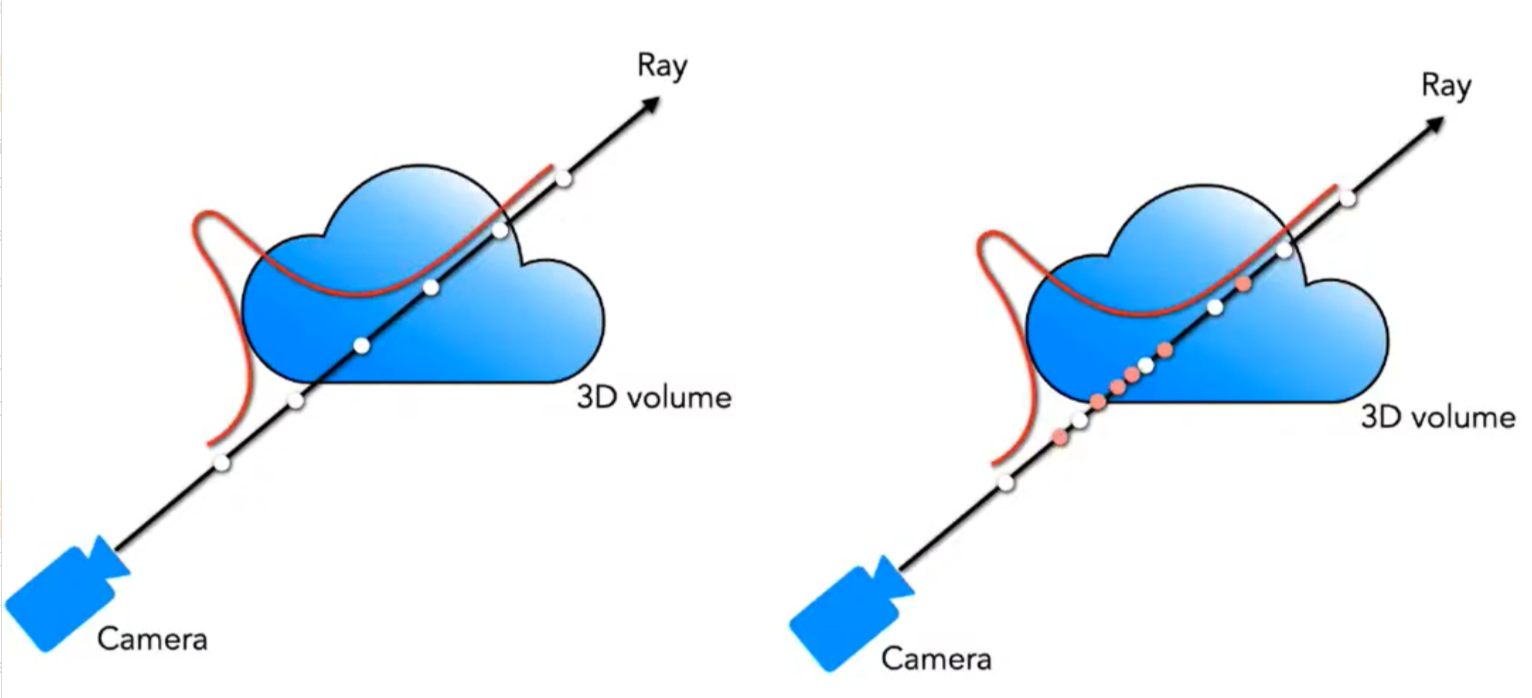
NeRF 的任务就是将一系列的微元采样点输入网络,计算体密度和颜色。那么微元的采样就成为一个关键的问题:采样点过多开销过大,采样点过少近似误差太大。直观的一个想法是,最好使得样本点分布在光线与物体相交的表面附近,而尽可能地避免在空缺部分以及被遮挡了的部分进行过多的采样,因为这些部分对最好的颜色贡献是很少的。
基于这一想法,NeRF 提出 Hierarchical volume sampling,即先按照均匀随机采样进行一次粗采样,将粗采样的输出的结果转化为分布,再根据分布进行一次精采样,最后 NeRF 训练的损失也是粗采样和精采样结果相加的结果。这样就实现了一个自动化 Coarse-To-Fine 的训练过程。如下图所示。
Coarse 阶段:
在 \([t_n,t_f]\) 中进行 stratified sampling 采样出 \(N_c\) 个位置,输入 coarse 网络,并将输出输入到第二阶段。
Fine 阶段:
考虑到离散化的渲染公式可视为沿着 ray 的所有采样颜色 \(c_i\) 的加权和
\[ \hat{C}(\mathbf{r})=\sum_{i=1}^{N_c}w_i\mathbf{c}_i,\quad w_i=T_i(1-\exp(-\sigma_i\delta_i)) \]
所以归一化权重 \(\hat{w}_i=\frac{w_i}{\sum_{j=1}^{N_c}w_j}\) 就是 \(\hat{C}(\mathbf{r})\) 在 ray 上的概率密度函数(PDF)。
因此,这一阶段基于 inverse transform sampling,在这个分布中采样出 \(N_f\) 个位置,然后将 \(N_c+N_f\) 采样得到的数据输入 fine 网络,并计算最终渲染的光线颜色 \(C(r)\)
这上述两阶段的采样达到了类似 importance sampling 的效果,但将采样点视为非均匀的离散化,而非对每个点进行独立的概率估计。
对每个场景都需要优化一个单独的 neural continuous volume representation network。需要优化的 \(L_2\) 损失为(同时优化 coarse 和 fine 网络):
\[ \mathcal{L}=\sum_{r\in\mathcal{R}}[||\hat{C}_c(\mathbf{r})-C(\mathbf{r})||_2^2+||\hat{C}_f(\mathbf{r})-C(\mathbf{r})||_2^2] \]
其中
- \(\mathcal{R}\):ray 的集合;
- \(C(\mathbf{r})\):ground truth RGB;
- \(\hat{C}_c(\mathbf{r})\):coarse volume predicted RGB;
- \(\hat{C}_f(\mathbf{r})\):fine volume predicted RGB;
虽然 Coarse-MLP 和 Fine-MLP 仅在样本点的输入上有所不同(同样的 Positional Encoding 和 MLP),但其样本点的分布本身就决定了各自 MLP 能够在何种程度“看到”低频和高频信号。Coarse-MLP 的样本点是光线在 near/far 区间上的均匀采样,这意味着这条光线上样本点的高频信号失真了(远处的也会包含高频信号);而 Fine-MLP 是在表面交点附近的密集采样,这意味着 MLP 能够密集地“感受”到这一段区域的高频信号(尽可能保证不失真)。
可以理解为采用不同的采样策略就是施加了不同的“滤波器”。对同一条光线,两组不同的采样使得 MLP “看到”截然不同的两组信号;如果想让一个 MLP 同时处理好这两组截然不同的信号,可能得高超的调参技巧与更大的网络了。
指标
NeRF 使用了 PSNR,SSIM,LPIPS 三个指标。关于这三个指标的详细信息,可参考图像评价指标。
拍摄场景
- 物体在中央,相机在四周拍摄,往往用于重建主体;
- 相机方向固定,在小范围移动;
- 类似全景图拍摄,相机在中间,朝各个方向拍摄,通常用于重建背景;
- 在固定空间内随机方向和分布拍摄;
- 是 1 和 3 的结合,既重建物体主体,又重建背景。

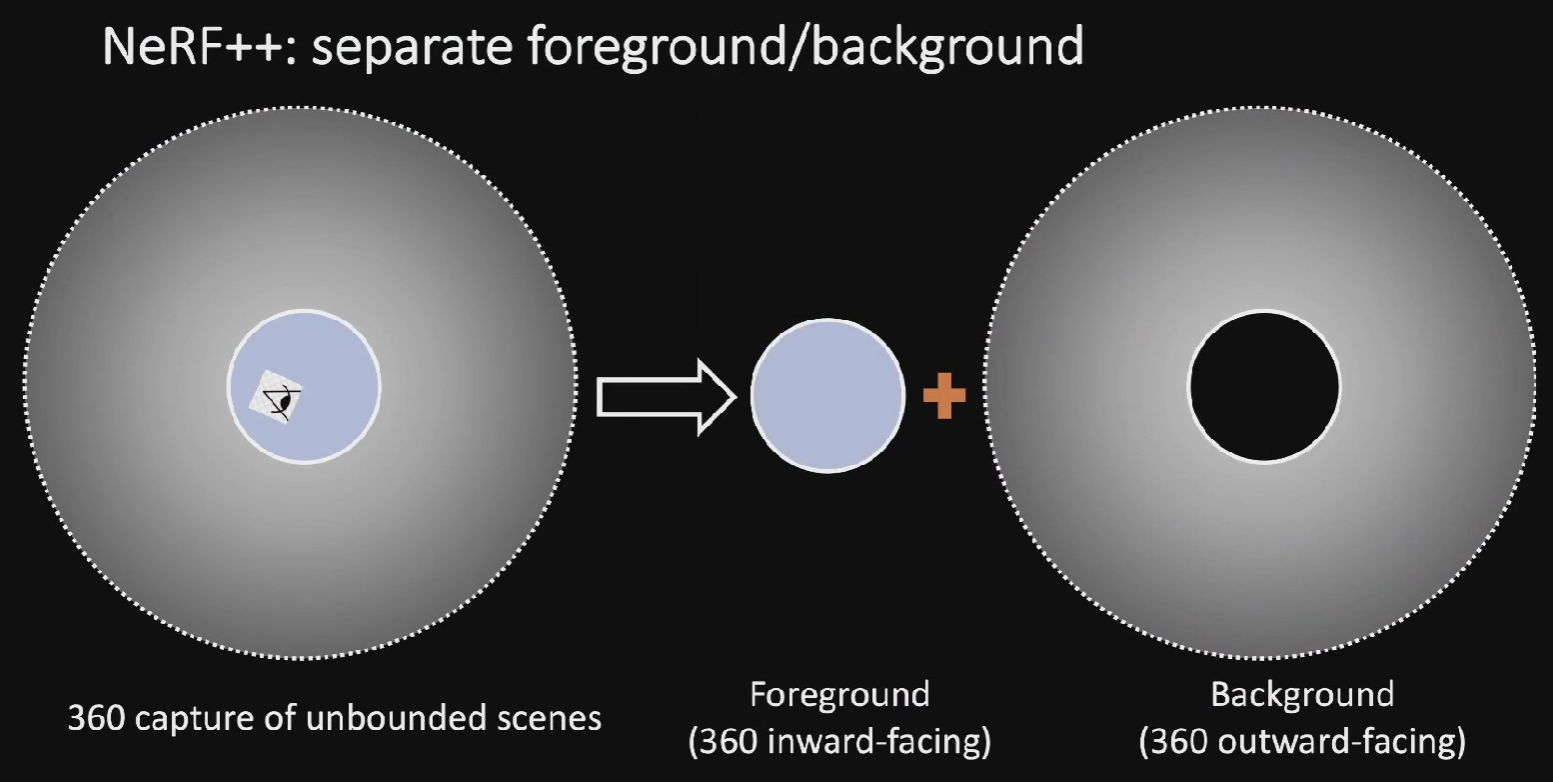
目前 NeRF 需要解决的问题就是,在空间内重建近景时远景会模糊,反之重建远景的时候近景会模糊。
为了解决这一问题,NeRF++ 提出了一种解决方案,即将 NeRF 进行分解和组合,在近景(Foreground)和远景(Background)处都分别使用一个 NeRF 来进行表征,最后再组合(combined)到一起。这也就是第五种拍摄场景。
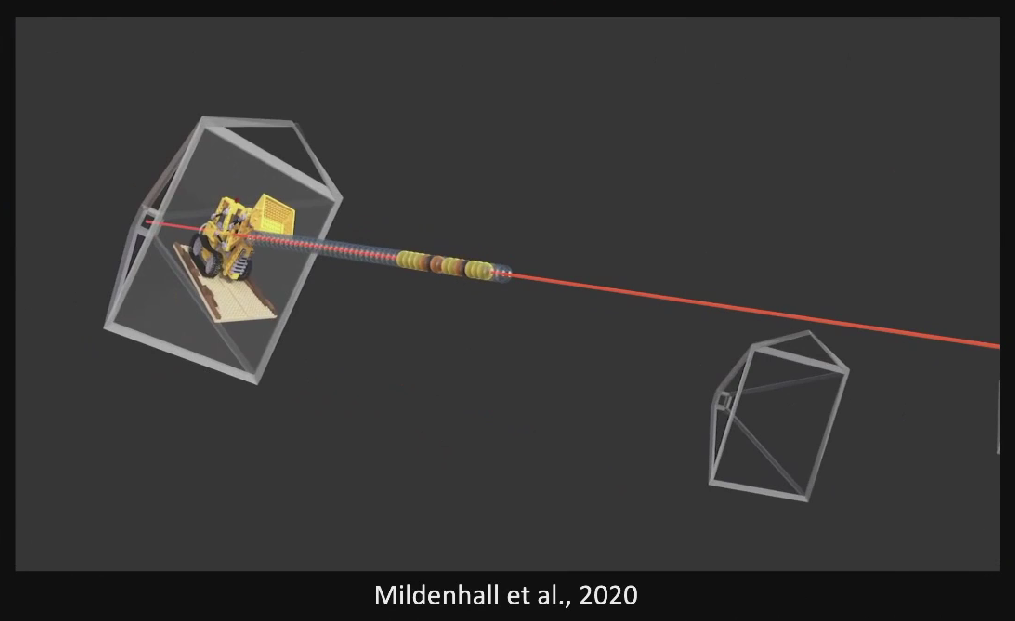
NeRF 实现的几个关键部分:
- 有一个三维空间,用一个连续的场表示;
- 空间里存在一个感兴趣的物体区域;
- 处于不同位置和朝向的相机拍摄多视角图像;
- 对于一张图像,根据相机中心和图像平面的一个像素点,两点确定一条射线穿过三维空间;
- 在射线上采样多个离散的三维点并利用体素渲染像素的颜色。
这里面涉及到了三维空间、物体区域、相机位置和朝向、图像、射线、以及三维采样点等。要想优化 NeRF,我们需要能够表达刚刚提到的这些东西,这就涉及到了如何将拍摄的数据进行转化。
关于如何正确转换相机参数和坐标系,可详见于相机参数与坐标系变换。