向量 (Vector)
定义
数域 \(F\) 上的 \(n\) 个数 \(a_1,a_2,...,a_n\) 所组成的有序数组 \([a_1,a_2,...,a_n]\) 称为 \(n\) 维向量,其中第 \(i\) 个数称为该向量的第 \(i\) 个分量. 通常用加粗小写字母 \(\mathbf{a}\),\(\mathbf{b}\) 表示.
概念
- 行向量:\(\mathbf{\alpha}=(a_1,a_2,...,a_n)\)
- 列向量:\(\mathbf{\beta}=\left(\begin{matrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{matrix}\right)=(b_1,b_2,...,b_n)^T\)
向量的线性运算
对向量 \(\mathbf{a}=(a_1,a_2,...,a_n)\) 和 \(\mathbf{b}=(b_1,b_2, b_n)\),有
- 相等
\[ \mathbf{a}=\mathbf{b} \Leftrightarrow a_i=b_i(i=1,2,...,n) \]
- 加法
\[ \mathbf{a}\pm\mathbf{b}=(a_1\pm b_1,a_2\pm b_2,...,a_n\pm b_n) \]
- 数乘
\[ k\mathbf{a}=(ka_1,ka_2,...,ka_n) \]
- 运算律
- \(\mathbf{a}+\mathbf{b}=\mathbf{b}+\mathbf{a}\)
- \((\mathbf{a}+\mathbf{b})+\mathbf{c}=\mathbf{a}+(\mathbf{b}+\mathbf{c})\)
- \(k(\mathbf{a}+\mathbf{b})=k\mathbf{a}+k\mathbf{b}\)
- \((k+l)\mathbf{a}=k\mathbf{a}+l\mathbf{a}\)
模与角度 (Norm and Angle)
向量内积
- 定义
给定 \(\mathbb{R}^n\) 中的向量 \(\mathbf{a}=(a_1,a_2,...,a_n)^T, \mathbf{b}=(b_1,b_2, b_n)^T\),称实数
\[ \sum_{i=1}^na_ib_i=a_1b_1+a_2b_2+...+a_nb_n \]
为 \(\mathbf{a}\) 和 \(\mathbf{b}\) 的内积,记为 \(\mathbf{a}^T\mathbf{b}\) .
- 运算性质
设 \(\alpha, \beta, \gamma\) 为 \(\mathbb{R}^n\) 中的向量,\(k\) 为实数:
- \(\alpha^T\beta=\beta^T\alpha\)
- \((k\alpha)^T\beta=k(\alpha^T\beta)=\alpha^T(k\beta)\)
- \((\alpha+\beta)^T\gamma=\alpha^T\gamma+\beta^T\gamma\)
- \(\alpha^T\alpha=0\Leftrightarrow\alpha=\mathbf{0}\)
向量的模
- 定义
给定 \(\mathbb{R}^n\) 中的向量 \(\mathbf{a}=(a_1,a_2,...,a_n)^T, \mathbf{b}=(b_1,b_2, b_n)^T\),称实数
\[ \sqrt{\mathbf{a}^T\mathbf{a}}=\sqrt{a_1^2+a_2^2+...+a_n^2}=\sqrt{\sum_{i=1}^na_i^2} \]
为向量 \(\mathbf{a}\) 的长度,记作 \(||\mathbf{a}||\)
- 性质
- 非负性:\(||\mathbf{a}||\geq 0\)
- 齐次性:\(||k\mathbf{a}||=|k|\cdot||\mathbf{a}||\)
- 柯西不等式:
\[ \begin{align*} &\left|\sum_{i=1}^na_ib_i\right|\leq\sqrt{\sum_{i=1}^na_i^2}\sqrt{\sum_{i=1}^nb_i^2} \\ \Leftrightarrow \quad& |\mathbf{a}^T\mathbf{b}|\leq||\mathbf{a}||\cdot||\mathbf{b}|| \end{align*} \]
等号成立当且仅当 \(\mathbf{a}\) 和 \(\mathbf{b}\) 线性相关。
- 若向量 \(\mathbf{a}\) 的模为 \(1\),则称 \(\mathbf{a}\) 为单位向量。设非零向量 \(\mathbf{a}\),令 \(\eta=\frac{\mathbf{a}}{||\mathbf{a}||}\),则 \(||\eta||=1\),且方向与 \(\mathbf{a}\) 相同。
向量夹角
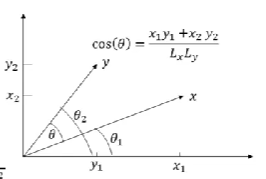
- 定义
若 \(x=(x_1,x_2)^T, y=(y_1,y_2)^T\),则
\[ \begin{align} &L_x=||x||=\sqrt{x_1^2+x_2^2},\quad L_y=||y||=\sqrt{y_1^2+y_2^2} \\ &\cos{\theta_1}=\frac{x_1}{||x||},\quad \cos{\theta_2}=\frac{y_1}{||y||} \\ &\sin{\theta_1}=\frac{x_2}{||x||},\quad \sin{\theta_2}=\frac{y_2}{||y||} \\ \cos{\theta}&=\cos{(\theta_2-\theta_1)}=\cos{\theta_2}\cos{\theta_1}+\sin{\theta_2}\sin{\theta_1}\notag \\ &=\frac{x_1y_1+x_2y_2}{||x||\cdot||y||}=\frac{x^Ty}{||x||\cdot||y||} \end{align} \]
向量正交(orthogonal)
- 定义
若两个 \(n\) 维向量 \(\mathbf{a}\) 和 \(\mathbf{b}\) 满足
\[ \mathbf{a}^T\mathbf{b}=a_1b_1+a_2b_2+...+a_nb_n=0 \]
则称 \(\mathbf{a}\) 和 \(\mathbf{b}\) 正交.
- 性质
- 零向量与任何向量都正交
- 与自身正交的向量只有零向量
- 正交向量组
若非零向量组 \((\mathbf{a}_1,\mathbf{a}_2,...,\mathbf{a}_n)\) 中,向量两两正交,即 \(\mathbf{a}_i^T\mathbf{a}_j=0 (i\neq j)\),则称该向量组为正交向量组.
泰勒公式与线性化
定义
若函数 \(f(x)\) 在 \(x_0\) 处有 \(n+1\) 阶导数,则存在 \(x_0\) 的一个邻域,对于该邻域内任一 \(x\),有
\[ f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f^{(2)}(x_0)}{2!}(x-x_0)^2+…+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) \]
该式子称为函数 \(f(x)\) 在 \(x_0\) 的泰勒公式. 其中,\(R_n(x)=o((x-x_0)^n)\) 称为拉格朗日余项,表示用 \(n\) 次泰勒多项式来近似表示 \(f(x)\) 所产生的误差. \(R_n(x)\)的具体表示为:
\[ R_n(x)=\frac{f^{n+1}(\xi)}{(n+1)!}(x-x_0)^{n+1}\quad (\xi \in (x_0,x)) \]
当 \(n=0\) 时,是拉格朗日中值公式:
\[ f(x)=f(x_0)+f'(\xi)(x-x_0)\quad (\xi \in (x_0,x)) \]
当 \(x_0=0\) 时,是麦克劳林公式:
\[ f(x)=f(0)+f'(\xi)x+\frac{f^{(2)}(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n+R_n(x)\quad (\xi \in (x_0,x)) \]
Jacobian 矩阵
n 维欧氏空间
定义
所有 \(n\) 个有序实数组 \((x_1,x_2,…,x_n)\) 的全体称为 \(n\) 维向量空间,或简称 \(n\) 维空间,其中每个有序实数组称为 \(n\) 维空间中的一个向量(或一个点),记作
\[ x=(x_1,x_2,…,x_n)^T \]
设 \(x=(x_1,x_2,…,x_n)^T\) 与 \(y=(y_1,y_2,…,y_n)^T\) 是 \(n\) 维空间中的任意两个向量,则向量 \(x\) 与 \(y\) 的内积定义为:
\[ x^Ty=x_1y_1+x_2y_2+…+x_ny_n \]
定义了内积的 \(n\) 维空间叫做 \(n\) 维欧几里得空间(简称 \(n\) 维欧式空间),记作 \(R^n\),利用内积定义向量 \(x \in R^n\) 的模为:
\[ |x|=\sqrt{x^Tx}=\sqrt{\sum_{i=1}^nx_i^2} \]
向量函数与实值函数
- 实值函数
即 \(n\) 维空间中的点集到实数集的映射(\(R^n \rightarrow R\)
- 向量函数
即 \(n\) 维欧氏空间中的点集到 \(m\) 维欧氏空间点集的映射(\(R^n \rightarrow R^m\)) 一般地,当 \(f_1,f_2,…,f_m\) 为 \(f\) 的分量函数(或坐标函数)时,可写作
\[ f(x)=\left(\begin{array}{c} f_1 \\ \vdots \\ f_m \end{array}\right)=\left(\begin{array}{c} f_1(x) \\ \vdots \\ f_m(x) \end{array}\right)=\left(\begin{array}{c} f_1(x_1,x_2,…,x_n) \\ \vdots \\ f_m(x_1,x_2,…,x_n) \end{array}\right) \]
两个相同维数的向量函数 \(f\) 和 \(g\) 在相同的定义域上的和(差)函数为:
\[ f \pm g =\left(\begin{array}{c} f_1 \pm g_1 \\ \vdots \\ f_n \pm g_n \end{array}\right) \]
一个实值函数 \(\alpha\) 向量函数 \(f\) 在相同的定义域上的乘积函数为:
\[ \alpha f =\left(\begin{array}{c} \alpha f_1 \\ \vdots \\ \alpha f_n \end{array}\right) \]
两个向量函数 \(f\) 和 \(h\) 的复合函数为:
\[ h \cdot f =\left(\begin{array}{c} h_1 \cdot f \\ \vdots \\ h_n \cdot f \end{array}\right) \]
梯度
分类
根据自变量和因变量的不同可分为:
自变量为实向量的标量函数 \(f\) 关于向量的梯度: 函数 \(f\) 关于行向量 \(x^T\) 的梯度为:
\[ \frac{\partial f}{\partial x^T} = [\frac{\partial f}{\partial x_1},...,\frac{\partial f}{\partial x_n}] = \nabla_{x^T}f(x) \]
函数 \(f\) 关于列向量 \(x\) 的梯度计算公式为:
\[ \frac{\partial f}{\partial x} = [\frac{\partial f}{\partial x_1},...,\frac{\partial f}{\partial x_n}]^T = \nabla_{x}f(x) \]
若 \(f\) 为常数,则对应的梯度为 \(\mathbf{0}\).
自变量为实向量(\(x_{n \times 1}\))的向量函数 \(f\) 关于向量的梯度:
\[ f \in R^m, \nabla_xf = \left[\begin{matrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_2}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_1} \\ \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_1}{\partial x_n} & \frac{\partial f_2}{\partial x_n} & \cdots & \frac{\partial f_m}{\partial x_n} \end{matrix}\right] = \frac{\partial f}{\partial x} \]
自变量为矩阵(\(x_{m \times n}\))的标量函数 \(f\) 关于矩阵的梯度:
\[ f \in R, \nabla_Xf = \left[\begin{matrix} \frac{\partial f_1}{\partial x_{11}} & \frac{\partial f_2}{\partial x_{12}} & \cdots & \frac{\partial f_m}{\partial x_{1n}} \\ \frac{\partial f_1}{\partial x_{21}} & \frac{\partial f_2}{\partial x_{22}} & \cdots & \frac{\partial f_m}{\partial x_{2n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_1}{\partial x_{m1}} & \frac{\partial f_2}{\partial x_{m2}} & \cdots & \frac{\partial f_m}{\partial x_{mn}} \end{matrix}\right] = \frac{\partial f}{\partial X} \]
运算法则
- 加法法则:若 \(f(x),g(x)\) 均为 \(x\) 的实值函数,则
\[ \frac{\partial[pf(x)+qg(x)]}{\partial x}=p\frac{\partial f(x)}{\partial x}+q\frac{\partial g(x)}{\partial x} \]
- 乘法法则:若 \(f(x),g(x)\) 均为 \(x\) 的实值函数,则
\[ \frac{\partial[f(x)g(x)]}{\partial x}=f(x)\frac{\partial g(x)}{\partial x}+g(x)\frac{\partial f(x)}{\partial x} \]
- 除法法则:若 \(f(x)\) 为向量 \(x\) 的向量值函数,则
\[ \frac{\partial[f(x)/g(x)]}{\partial x}=\frac{1}{g^2(x)}\left[g(x)\frac{\partial f(x)}{\partial x}-f(x)\frac{\partial g(x)}{\partial x}\right] \]
- 链式法则:若\(g(x)\)为\(x\)的向量值函数,则
\[ \frac{\partial g(f(x))}{\partial x}=\frac{\partial g(f)}{\partial f}\frac{\partial f(x)}{\partial x} \]
- 常见类型的梯度 \[ \begin{align*} \nabla(x^Tx)=\frac{\partial x^Tx}{\partial x} = 2x,\quad \nabla(a^Tx)=\frac{\partial a^Tx}{\partial x} = a,\\ \nabla(x^TA)=\frac{\partial x^TA}{\partial x} = A,\quad \nabla(x^TAx)=\frac{\partial x^TAx}{\partial x} = (A+A^T)x \end{align*} \]
Jacobian 矩阵
若函数 \(f(x):\mathbb{R}^n \rightarrow \mathbb{R}^m\),有:
\[ x=[x_1,x_2,…,x_n]^T, f(x)=\left[\begin{array}{c} f_1(x_1,x_2,…,x_n) \\ f_2(x_1,x_2,…,x_n) \\ \vdots \\ f_m(x_1,x_2,…,x_n) \end{array}\right] \]
则 Jacobian 矩阵 \(J(x)\) 可以写为:
\[ f \in \mathbb{R}^{m \times 1}, J(x) =\left[\begin{matrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n} \end{matrix}\right] = \nabla_x^T f \]
Jacobian 矩阵表现了向量函数的最佳线性逼近,也即
\[ f(x) \approx f(p) + J(p)(x-p) \]
Hessian 矩阵
若 \(f:\mathbb{R}^n \rightarrow \mathbb{R}\) 为二次可导函数,\(x=[x_1,x_2,…,x_n]^T\),则 \(f\) 的Hessian矩阵为:
\[ H(f)=\left[\begin{matrix} \frac{\partial^2 f}{\partial x_1 \partial x_1} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n \partial x_n} \end{matrix}\right] =\nabla_x^2f \]
Hessian矩阵使用了函数的二阶信息,常用于解决优化问题。当 \(f\) 的二阶混合偏导数连续时,它是一个对称矩阵。这时,\(f\) 在 \(x_0\) 的二阶泰勒公式可简单地写成:
\[ f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2}(x-x_0)^Tf^2(x_0)(x-x_0)+o(|x-x_0|^2) \]
贝叶斯决策理论和 HMM
贝叶斯决策理论
贝叶斯定理
设 \(n\) 个事件 \(A_1,A_2,…,A_n\) 两两互斥,\(A_1+A_2+…+A_n=\Omega\)(满足这两个条件的事件组称为一个完备事件组),且 \(P(A_i)>0(i=1,2,…,n)\) 则
\[ P(A_i|B)=\frac{P(A_i)P(B|A_i)}{\sum_{j=1}^nP(A_i)P(B|A_j)} \]
\(P(A_i|B)\) 是在事件 \(B\) 发生的条件下,某个原因 \(A_i\) 发生的概率,称为后验概率,称 \(P(A_i)\) 为先验概率.
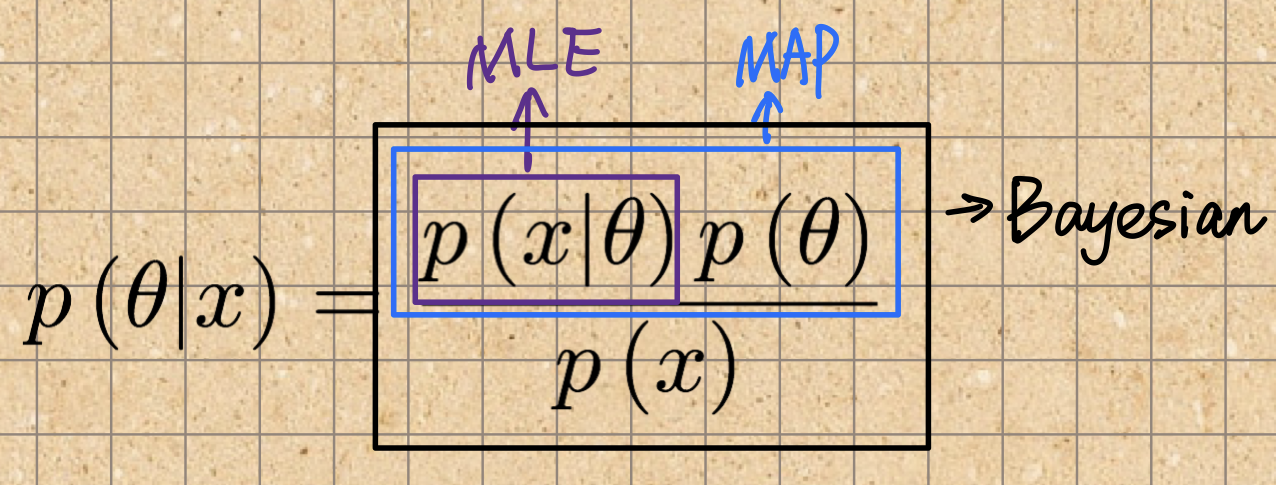
MLE、MAP 和 Bayesian
令:
- \(D={(x_1,y_1),…,(x_n,y_n)}\) 表示训练样本集
- \(\theta\) 表示模型所有的参数
- \(x^*\) 表示一个新的样本(训练完的模型需要做预测),\(\hat y\) 表示模型对新样本的预测值
最大似然估计(Maximum likelihood estimation, MLE)
- 在给定一个模型参数的情况下,计算样本集的概率 \(p(D|\theta)\)
- 目标是找到最优的参数 \(\theta^*\)使得\(p(D|\theta)\) 最大化
- 预测 \(p(\hat y|x^,\theta^)\)
目标:
\[ \theta^{MLE}=\arg\max\theta p(D|\theta) \]
要找到最优参数 \(\theta^{MLE}\) 使得 \(p(D|\theta)\) 最大化,通常可通过令导数等于0等到:
\[ \frac{\partial p(D|\theta)}{\partial \theta}=0 \]
MLE 未考虑到先验,且容易造成过拟合.
最大后验估计(Maximum a posteriori estimation,MAP)
- 在给定样本的情况下,计算参数的概率 \(p(\theta|D)\)
- 目标是找到最优的参数 \(\theta^*\) 使得 \(p(\theta|D)\) 最大化
- 预测 \(p(\hat y|x^,\theta^)\)
目标:
\[ \theta^{MAP}=\arg\max\theta p(\theta|D) \]
根据贝叶斯公式有:
\[ p(\theta|D)=\frac{p(D|\theta)p(\theta)}{p(D)} \]
目标可以转为:
\[ \theta^{MAP}=\arg\max\theta p(D|\theta)p(\theta) \]
进一步取对数形式:
\[ \theta^{MAP}=\arg\max\theta \log p(D|\theta)+\log p(\theta) \]
MAP 与 MLE 最大不同在于 \(p(\theta)\) 项,MAP 解决了 MLE 缺乏先验的缺点.
贝叶斯估计(Bayesian estimation)
- 在给定样本的情况下,计算参数的分布 \(p(\theta|D)\)
- 预测 \(p(\hat y|x^*,D)=\int_\theta p(\hat y|x^*,\theta)p(\theta|D)d\theta\)
目标:
对于一个新样本\(x^*\),模型的预测为:
\[ p(\hat y|x^*,D)=\int_\theta p(\hat y|x^*,\theta)p(\theta|D)d\theta \]
需要计算后验概率 \(p(\theta|D)\):
\[ p(\theta|D)=\frac{p(D|\theta)p(\theta)}{\int p(D|\theta)p(\theta)d\theta} \]
后验概率需要近似计算.
蒙特卡洛方法
通过随机抽样方法,以随机事件出现的频率估计其概率,或者以抽样的数字特征估算随机变量的数字特征,并将其作为问题的解。
隐马尔科夫模型(Hidden Markov Model, HMM)
- 一种简单的有向图模型,常用于处理时间序列数据
- 在多个领域应用广泛:语音识别、自然语言处理、词性标注等等
变量
HMM的变量分为两种:
- 因变量 \(y \in Y\) :在\(i\)时刻系统所处的状态(通常离散型)
- 观察变量 \(x \in X\) :在\(i\)时刻所处的观察值(离散、连续)
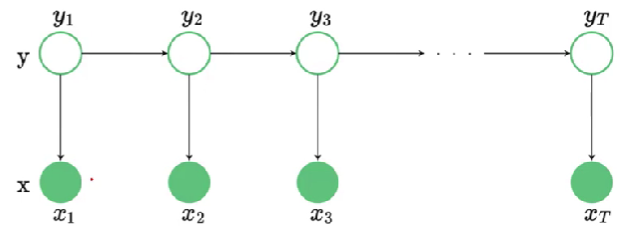
状态
下一个状态仅由当前状态决定,与其他状态变量无关.
\(x\) 在给定 \(y\) 的情况下条件独立,HMM 中因变量和观察变量的联合分布可以写为
\[ \begin{align*} p(\textbf{x}^n,\textbf{y}^n)=p(y_1)p(x_1|y_1)\prod_{t=2}^Tp(x_t|y_t)p(y_t|y_{t-1})\\ \textbf{x}^n=(x_1,x_2,...,x_T),\quad \textbf{y}^n=(y_1,y_2,...,y_T) \end{align*} \]