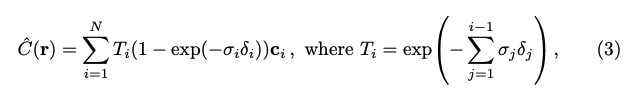体渲染
体渲染属于整个渲染技术的分支,它的目的主要是为了解决云、烟、果冻这类非刚性物体的渲染建模,可以简单理解为是为了处理密度较小的非固体的渲染。
为了建模这种非刚性物体的渲染,体渲染把气体等物质抽象成一团飘忽不定的粒子群。光线在穿过这类物体时,其实就是光子在跟粒子发生碰撞的过程。
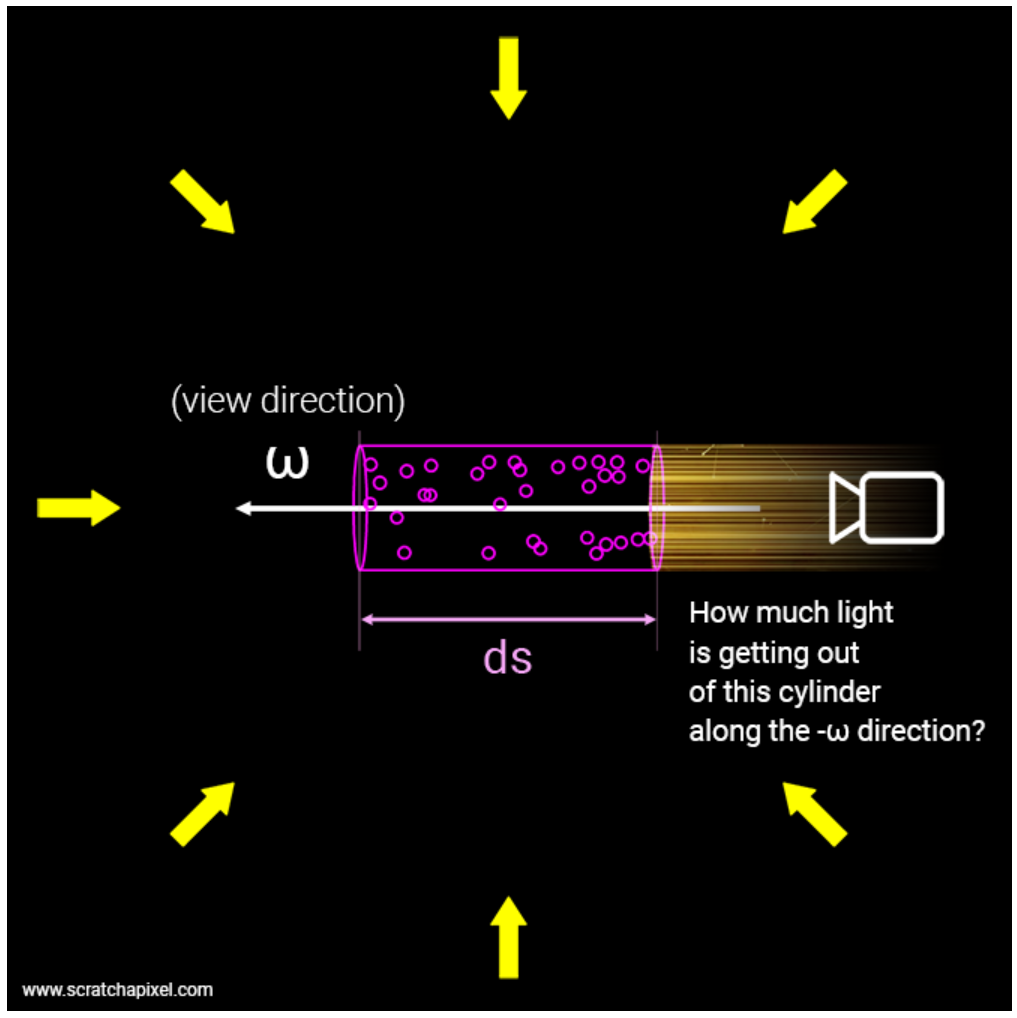
下图是体渲染建模的示意图。光沿直线方向穿过一堆粒子 (粉色部分),如果能计算出每根光线从最开始发射,到最终打到成像平面上的辐射强度,我们就可以渲染出投影图像。而体渲染要做的,就是对这个过程进行建模。为了简化计算,我们就假设光子只跟它附近的粒子发生作用,这个范围就是图中圆柱体大小的区间。
体渲染把光子与粒子发生作用的过程,进一步细化为四种类型:
- 吸收 (absorption):光子被粒子吸收,会导致入射光的辐射强度减弱;
- 放射 (emission):粒子本身可能发光,比如气体加热到一定程度就会离子化,变成发光的「火焰」。这会进一步增大辐射强度;
- 外散射 (out-scattering):光子在撞击到粒子后,可能会发生弹射,导致方向发生偏移,会减弱入射光强度;
- 内散射 (in-scattering):其他方向的光子在撞到粒子后,可能和当前方向上的光子重合,从而增强当前光路上的辐射强度。
下图是这四种情况的示意图,\(L_i\) 表示入射光,\(L_o\) 表示出射光。
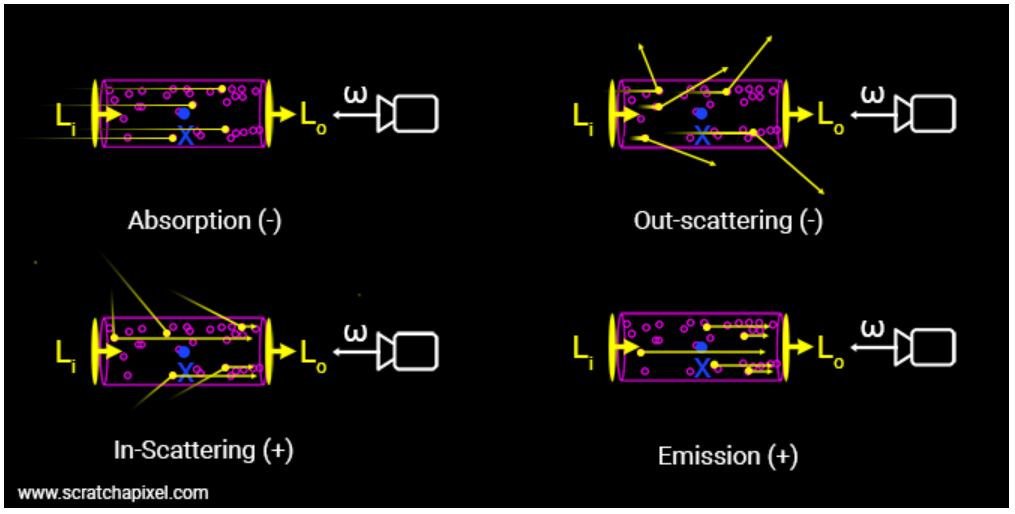
出射光与入射光之间的变化量,可以表示为这四个过程的叠加:
\[ dL(x,w)=\text{emission}+\text{inscattering}-\text{outscattering}-\text{absorption} \]
其中 \(x\) 表示光线上某个位置点,\(w\) 表示光线发射方向。
吸收 (absorbing)
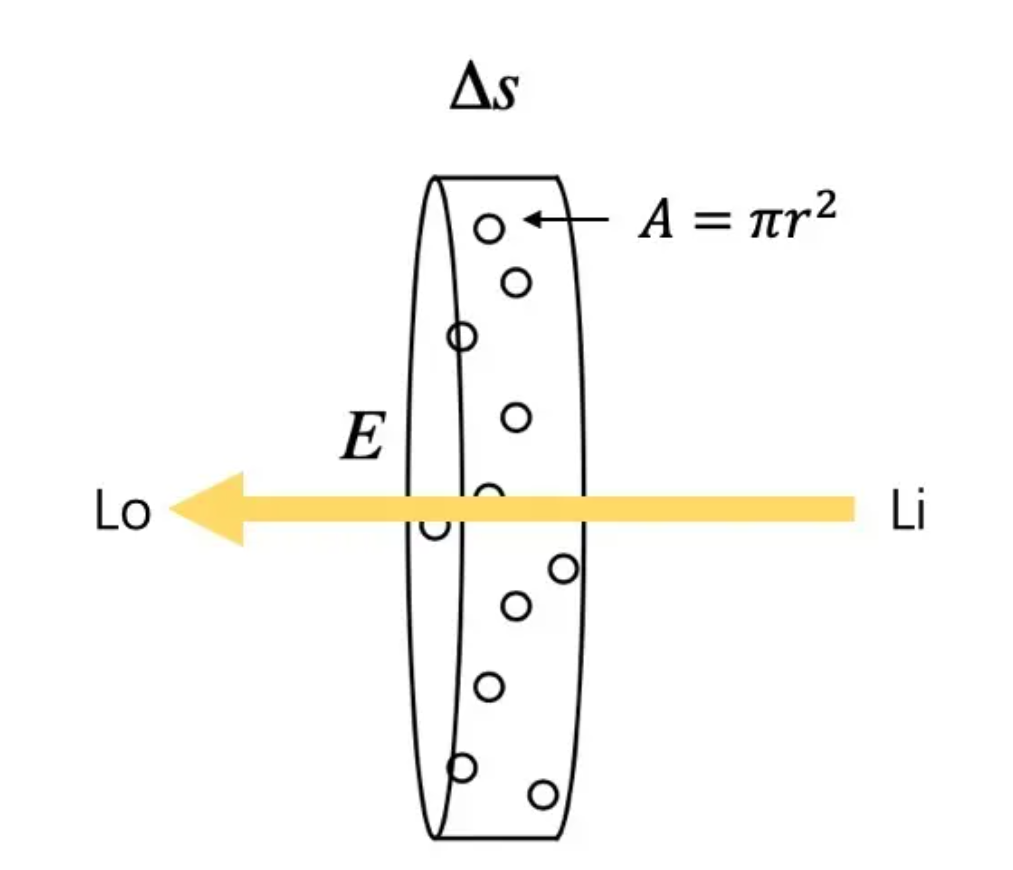
假设粒子都是半径为 \(r\) 的球体,那么每个粒子的投影面积是 \(A=\pi r^2\) (也就是每个粒子对光线的遮挡面积)。假设圆柱体中粒子的密度是 \(\rho\),圆柱体的底面积是 \(E\)。
当圆柱体足够薄 (薄到跟粒子一样厚) 的时候,可以认为粒子之间不会互相重叠 (也就是粒子都平铺在圆柱体一个横截面上)。
假定这个厚度是 \(\Delta s\),那么在这个厚度内,圆柱体体积为 \(E\Delta s\),粒子总数为 \(\rho E\Delta s\)。这些粒子遮挡的面积为 \(\rho E\Delta sA\),占整个底面积的比例为 \(\rho E\Delta sA/E=\rho A\Delta s\)。也就是说,当一束光通过这个圆柱体的时候,有 \(\rho A\Delta s\) 的概率会被遮挡。
换句话说,如果我们在圆柱体的一端发射无数光线 (假设都朝相同的方向),在另一端接收,会发现有些光线安然通过,有些则被粒子遮挡 (吸收)。整体上,这些接受到的光线总强度,相比入射光线总强度而言,会有 \(\rho A\Delta s\) 比例的衰减,即出射光的强度均值是入射光的 \(\rho A\Delta s\) 倍。
\[ \begin{align} I_o-I_i=\Delta I=-\rho(s)AI(s)\Delta s\notag \\ \implies dI=-\rho(s)AI(s)ds \end{align} \]
粒子密度 \(\rho\) 是一个关于 \(s\) 的函数,因为每个区域的密度都是不同的。
- 式可以转换为常微分方程:
\[ \begin{equation} \frac{dI}{ds}=-\rho(s)AI(s)=-\tau_a(s)I(s) \end{equation} \]
解这个方程可以得到:
\[ \begin{equation} I(s)=I_0\exp(-\int_0^s\tau_a(t)dt) \end{equation} \]
公式里面的 \(I_0\) (注意区分 \(I_o\)) 是常微分方程中的常数项,物理意义上表示光线的起始点。而 \(I_o\) 应为 \(I_o=I_i\exp(-\int_i^o\tau_a(t)dt)\)
如果介质 (粒子群) 是均匀的,即 \(\tau_a(t)\) 处处相等,那么入射光在经过介质 (粒子群) 后,辐射强度会呈指数衰减。这被称为比尔-朗伯吸收定律 (Beer-Lambert Law):
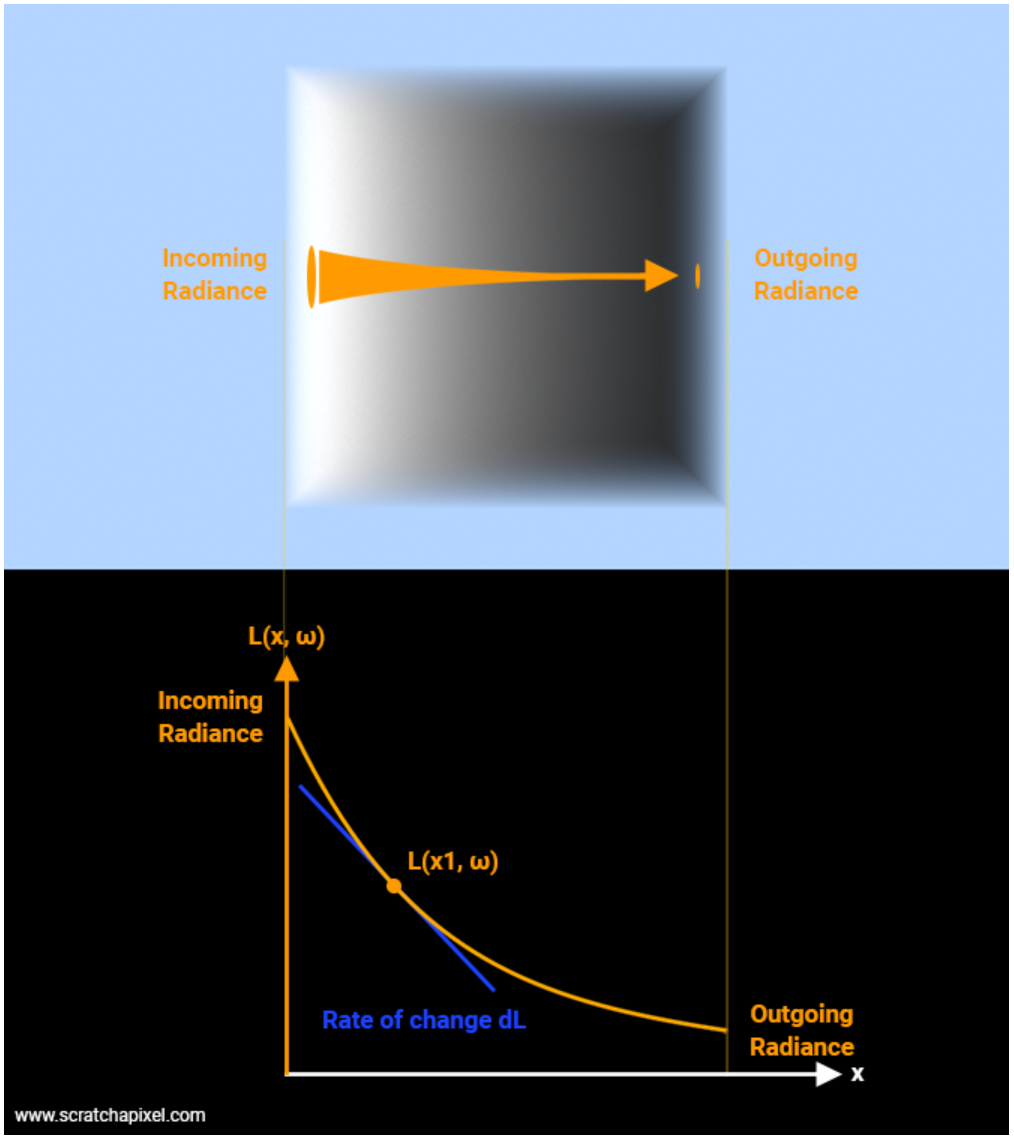
可以由此定义透射比 (transmittance):
\[ \begin{equation} T(s)=\frac{I_o}{I_i}=\exp(-\int_i^o\tau_a(t)dt) \end{equation} \]
它表示粒子群某一点的透明度,数值越大,说明粒子群越透明,光线衰减的幅度就越小。
而透明度本身是关于 \(\tau_a(t)\) 的方程,\(\tau_a(t)\) 越大,\(T(s)\) 就越小。由公式 (2) 可知,\(\tau_a(t)=\rho(t)A\),它是由粒子密度和投影面积决定的。这在直觉上也很好理解,如果粒子密度大,粒子本身也比较大,那么遮住光线的概率也会相应提升,自然透明度也就下降了。
\(\tau_a(t)\) 也被称为光学厚度 (optical depth)。

放射 (emission)
除了吸收之外,粒子本身也可能发光。
假设单个粒子发射一束光的辐射强度为 \(I_e\),那么按照前文的描述,在圆柱体足够薄的情况下,粒子总数是 \(\rho AE\Delta s\),则总的发光强度为 \(I_e\rho AE\Delta s\)。
如果我们在圆柱体一端去接收粒子们放射的光线,会发现有时候能接收到,有时候刚好接收点所在的光路上没有粒子,就接收不到。能接收到光线的概率为 \(\rho AE\Delta s/E=\rho A\Delta s\),那么接收到的光线的平均强度为 \(I_e\rho A\Delta s\)。
同样地,可以得到放射光强的常微分方程:
\[ \begin{equation} \frac{dI}{ds}=I_e(s)\rho(s)A=I_e(s)\tau_a(s) \end{equation} \]
\(I_e\) 是一个关于 \(s\) 的函数,因为圆柱体不同位置的粒子,所放射的光强都是有差异的。这里我们也看到,类似吸收,粒子放射的光强同样和 \(\tau_a(s)\) 有关,这在直觉上也是合理的,如果粒子能发光,那粒子密度和粒子颗粒越大,放射的辐射均值也就越大。
外散射 (out-scattering)
粒子除了吸收光子,也可能会弹射光子,这个过程称为外散射,即光子被弹射出原本的光路,导致光线强度减弱。
同吸收一样,外散射对光线的「削弱」程度,也跟光学厚度相关,不过过程相对吸收来说又复杂一些,因此我们用 \(\tau_s\) 来表示外散射对光线的削弱比例,以区别于 \(\tau_a\)。
同样地,这一过程可以表示为:
\[ \begin{equation} \frac{dI}{ds}=-\tau_s(s)I(s) \end{equation} \]
内散射 (in-scattering)
光子可以被弹射走,自然就有其他光路的光子被弹射到当前光路,这一过程就是内散射。
内散射的过程比外散射又更加复杂,因为弹射到当前光路的光子可能来自多条不同的光路,因此需要综合考虑其他光路的辐射强度以及各种弹射角度。
不过本文不打算深入探究这一点,我们就认为其他光路的辐射强度为 \(I_s\),而弹射到当前光路的能量损失比为 \(\tau_s\) (注意这里和外散射使用的是相同的系数,既然都是散射,那有些性质上自然是共通的)。
内散射的过程可以表示为:
\[ \begin{equation} \frac{dI}{ds}=\tau_s(s)I_s(s) \end{equation} \]
体渲染方程
我们把以上四个过程都综合到一个公式中:
\[ \begin{equation} \frac{dI}{ds}=-\tau_a(s)I(s)-\tau_s(s)I(s)+\tau_a(s)I_e(s)+\tau_s(s)I_s(s) \end{equation} \]
其中,吸收和外散射都会削弱光线的辐射强度,并且由于它们都和入射光有关,因此它们共同构成了体渲染中的衰减项 (attenuation item),而粒子发光和内散射都来自独立的光源,因此被称为源项 (source item)。
为了求解方便,定义 \(\tau_t=\tau_a+\tau_s\),公式 (8) 就简化为:
\[ \begin{equation} \frac{dI}{ds}=-\tau_t(s)I(s)+\tau_a(s)I_e(s)+\tau_s(s)I_s(s) \end{equation} \]
求解这个微分方程,得到:
\[ \begin{equation} I(s)=\int_0^s\exp(-\int_0^t\tau_t(u)du)[\tau_a(s)I_e(s)+\tau_s(s)I_s(s)]dt+I_0\exp(-\int_0^s\tau_t(t)dt) \end{equation} \]
公式 (10) 就是体渲染的渲染方程了,其中 \(I_0\) 就是入射光最开始的强度,在 NeRF 中把它当作是背景光。
这个公式告诉我们,出射光的强度主要由入射光 (背景光) 和源项 (粒子发光以及内散射) 等构成的,而这两者在传递过程中都伴随着相同的衰减 (\(\tau_t\))。同时由于从 \(I_0\) 到 \(I_s\) 的整个光路上,处处都可能存在粒子发光和内散射现象,因此源项是需要从 \(0\) 开始相加一直到 \(s\) 的,对应到公式中就是积分 \(\int_0^s\)。
有了这个公式,我们就可以建模出每一条光线在传播介质中,辐射强度的变化,并最终渲染出图像 (当然前提要知道介质中每一点的 \(\tau_t\)、\(I_e\) 等信息)。
注意,虽然我们在讨论这个模型的时候一直是用辐射强度这个概念,但直接把 \(I(s)\) 替换成颜色也是可以的。
现在,我们做一个大胆的假设,假设 \(\tau_t\)、\(\tau_a\)、\(\tau_s\) 这些都相等,统一用 \(\sigma\) 表示,同时令 \(C=I_e+I_s\),那么公式 (10) 可以进一步简化成:
\[ \begin{align} I(s)&=\int_0^s\exp(-\int_0^t\sigma(u)du)\sigma(t)C(t)dt+I_0\exp(-\int_0^s\sigma(t)dt)\notag \\ &=\int_0^sT(t)\sigma(t)C(t)dt+I_0T(s) \end{align} \]
其中 \(T(t)=\exp(-\int_0^t\sigma(u)du)\)
计算机的体渲染
公式 (11) 在计算机中是无法表达的,需要进一步离散化。
我们将整个光路 \([0, s]\) 划分为 \(N\) 个相等间距的区间:\([t_n,t_{n+1}]\)。那么,只要能算出每个 \([t_n,t_{n+1}]\) 区间内的辐射强度 \(I(t_n\rightarrow t_{n+1})\),最后把 \(N\) 个区间的辐射加起来,就可以得到最终的光线强度了。\(N\) 越大,则越接近理论数值 (公式 (11))。
为了方便运算,我们假设在每个区间内,\(\sigma(t)\) 处处等于 \(\sigma_n\) ,\(C(t)\) 处处等于 \(C_n\)。那么可以得到:
\[ \begin{align} I(t_n\rightarrow t_{n+1})&=\int_{t_n}^{t_{n+1}}T(t)\sigma_nC_ndt \notag\\ &=\sigma_nC_n\int_{t_n}^{t_{n+1}}T(t)dt \end{align} \]
注意 \(T(t)=\exp(-\int_0^t\sigma(u)du)\),是需要从光线起点处开始积分的。不过,好在 \(T(t)\) 可以拆分为两段的乘积:
\[ \begin{align} T(t)&=\exp(-\int_0^t\sigma(u)du) \notag\\ &=\exp(-[\int_0^{t_n}\sigma(u)du+\int_{t_n}^t\sigma(u)du]) \notag\\ &=\exp(-\int_0^{t_n}\sigma(u)du)\exp(-\int_{t_n}^t\sigma(u)du) \notag\\ &=T(0\rightarrow t_n)T(t_n\rightarrow t) \end{align} \]
这样公式 (12) 就变成:
\[ \begin{align} I(t_n\rightarrow t_{n+1})&=\sigma_nC_n\int_{t_n}^{t_{n+1}}T(0\rightarrow t_n)T(t_n\rightarrow t)dt \notag\\ &=\sigma_nC_nT(0\rightarrow t_n)\int_{t_n}^{t_{n+1}}T(t_n\rightarrow t)dt \notag\\ &=\sigma_nC_nT(0\rightarrow t_n)\int_{t_n}^{t_{n+1}}\exp(-\int_{t_n}^t\sigma_ndu)dt \notag\\ &=\sigma_nC_nT(0\rightarrow t_n)\int_{t_n}^{t_{n+1}}\exp(-\sigma_nu|_{t_n}^t)dt \notag\\ &=\sigma_nC_nT(0\rightarrow t_n)\int_{t_n}^{t_{n+1}}\exp(-\sigma_n(t-t_n))dt \notag\\ &=\sigma_nC_nT(0\rightarrow t_n)\frac{\exp(-\sigma_n(t-t_n))}{-\sigma_n}|_{t_n}^{t_{n+1}} \notag\\ &=C_nT(0\rightarrow t_n)(1-\exp(-\sigma_n(t_{n+1}-t_n))) \end{align} \]
现在我们得到了 \(I(t_n\rightarrow t_{n+1})\),接下来就是把每一段得累加起来了:
\[ \begin{align} I(s)&=\int_0^sT(t)\sigma(t)C(t)dt+I_0T(s) \notag\\ &\approx\sum_{n=1}^NI(t_n\rightarrow t_{n+1})+I_0T(s) \notag\\ &=\sum_{n=1}^NC_nT(0\rightarrow t_n)(1-\exp(-\sigma_n(t_{n+1}-t_n)))+I_0T(s) \end{align} \]
假设 \(\delta_n=t_{n+1}-t_n\),那么 \(\delta_n\) 表示的就是每个小区间的长度,我们令 \(T_n=T(0\rightarrow t_n)\),则 \(T_n\) 也可以离散化为:
\[ \begin{align} T_n&=\exp(-\int_0^{t_n}\sigma(u)du) \notag\\ &\approx\exp(\sum_{k=1}^{n-1}-\sigma_k\delta_k) \end{align} \]
将公式 (16) 代入 (15) 后,可以得到最终计算机使用的体渲染公式:
\[ \begin{equation} I(s)=\sum_{n=1}^NT_n(1-\exp(-\sigma_k\delta_k))C_n+I_0T(s) \end{equation} \]
这个公式就是 NeRF 论文中公式 (3) 的出处,只不过加了背景光: